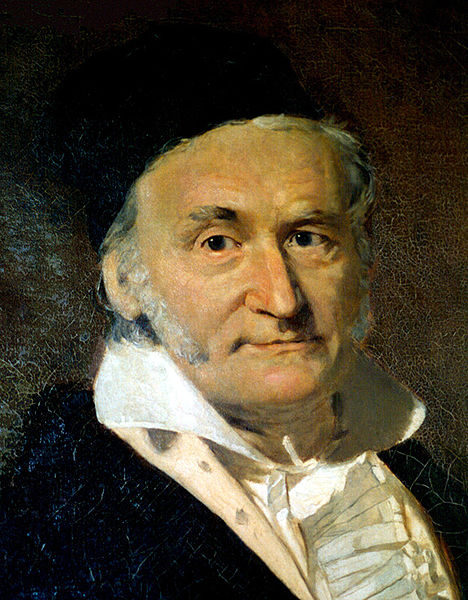
Johann Carl Friedrich Gauss (Latin: Carolus Fridericus Gauss) (30 April 1777 – 23 February 1855) was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics. Sometimes known as the Princeps mathematicorum (Latin, "the Prince of Mathematicians" or "the foremost of mathematicians") and "greatest mathematician since antiquity," Gauss had a remarkable influence in many fields of mathematics and science and is ranked as one of history's most influential mathematicians. He referred to mathematics as "the queen of sciences."

Gauss was a child prodigy. There are many anecdotes pertaining to his precocity while a toddler, and he made his first ground-breaking mathematical discoveries while still a teenager. He completed Disquisitiones Arithmeticae, his magnum opus, in 1798 at the age of 21, though it was not published until 1801. This work was fundamental in consolidating number theory as a discipline and has shaped the field to the present day.

Carl Friedrich Gauss was born on April 30, 1777 in Braunschweig, in the Electorate of Brunswick-Lüneburg, now part of Lower Saxony, Germany, as the son of poor working-class parents. He was christened and confirmed in a church near the school he attended as a child. There are several stories of his early genius. According to one, his gifts became very apparent at the age of three when he corrected, mentally and without fault in his calculations, an error his father had made on paper while calculating finances.

Carl's intellectual abilities attracted the attention of the Duke of Braunschweig, who sent him to the Collegium Carolinum (now Technische Universität Braunschweig), which he attended from 1792 to 1795, and to the University of Göttingen from 1795 to 1798. While in university, Gauss independently rediscovered several important theorems; his breakthrough occurred in 1796 when he was able to show that any regular polygon with a number of sides which is a Fermat prime (and, consequently, those polygons with any number of sides which is the product of distinct Fermat primes and a power of 2) can be constructed by compass and straightedge. This was a major discovery in an important field of mathematics; construction problems had occupied mathematicians since the days of the Ancient Greeks, and the discovery ultimately led Gauss to choose mathematics instead of philology as a career. Gauss was so pleased by this result that he requested that a regular heptadecagon be inscribed on his tombstone. The stonemason declined, stating that the difficult construction would essentially look like a circle.

The year 1796 was most productive for both Gauss and number theory. He discovered a construction of the heptadecagon on March 30. He invented modular arithmetic, greatly simplifying manipulations in number theory. He became the first to prove the quadratic reciprocity law on 8 April. This remarkably general law allows mathematicians to determine the solvability of any quadratic equation in modular arithmetic. The prime number theorem, conjectured on 31 May, gives a good understanding of how the prime numbers are distributed among the integers. Gauss also discovered that every positive integer is representable as a sum of at most three triangular numbers on 10 July and then jotted down in his diary the famous words, "Heureka! num = Δ + Δ + Δ." On October 1 he published a result on the number of solutions of polynomials with coefficients in finite fields, which ultimately led to the Weil conjectures 150 years later.

In his 1799 doctorate in absentia, A new proof of the theorem that every integral rational algebraic function of one variable can be resolved into real factors of the first or second degree, Gauss proved the fundamental theorem of algebra which states that every non-constant single-variable polynomial over the complex numbers has at least one root. Mathematicians including Jean le Rond d'Alembert had produced false proofs before him, and Gauss's dissertation contains a critique of d'Alembert's work. Ironically, by today's standard, Gauss's own attempt is not acceptable, owing to implicit use of the Jordan curve theorem. However, he subsequently produced three other proofs, the last one in 1849 being generally rigorous. His attempts clarified the concept of complex numbers considerably along the way.

Gauss also made important contributions to number theory with his 1801 book Disquisitiones Arithmeticae (Latin, Arithmetical Investigations), which contained a clean presentation of modular arithmetic and the first proof of the law of quadratic reciprocity. In that same year, Italian astronomer Giuseppe Piazzi discovered the dwarf planet Ceres, but could only watch it for a few days. Gauss predicted correctly the position at which it could be found again, and it was rediscovered by Franz Xaver von Zach on 31 December 1801 in Gotha, and one day later by Heinrich Olbers in Bremen. Zach noted that "without the intelligent work and calculations of Doctor Gauss we might not have found Ceres again." Though Gauss had been up to that point supported by the stipend from the Duke, he doubted the security of this arrangement, and also did not believe pure mathematics to be important enough to deserve support. Thus he sought a position in astronomy, and in 1807 was appointed Professor of Astronomy and Director of the astronomical observatory in Göttingen, a post he held for the remainder of his life.

The discovery of Ceres by Piazzi on 1 January 1801 led Gauss to his work on a theory of the motion of planetoids disturbed by large planets, eventually published in 1809 under the name Theoria motus corporum coelestium in sectionibus conicis solem ambientum (theory of motion of the celestial bodies moving in conic sections around the sun). Piazzi had only been able to track Ceres for a couple of months, following it for three degrees across the night sky. Then it disappeared temporarily behind the glare of the Sun. Several months later, when Ceres should have reappeared, Piazzi could not locate it: the mathematical tools of the time were not able to extrapolate a position from such a scant amount of data — three degrees represent less than 1% of the total orbit. Gauss, who was 23 at the time, heard about the problem and tackled it. After three months of intense work, he predicted a position for Ceres in December 1801—just about a year after its first sighting—and this turned out to be accurate within a half-degree. In the process, he so streamlined the cumbersome mathematics of 18th century orbital prediction that his work—published a few years later as Theory of Celestial Movement—remains a cornerstone of astronomical computation. It introduced the Gaussian gravitational constant, and contained an influential treatment of the method of least squares, a procedure used in all sciences to this day to minimize the impact of measurement error. Gauss was able to prove the method in 1809 under the assumption of normally distributed errors. The method had been described earlier by Adrien-Marie Legendre in 1805, but Gauss claimed that he had been using it since 1795.

Gauss was a prodigious mental calculator. Reputedly, when asked how he had been able to predict the trajectory of Ceres with such accuracy he replied, "I used logarithms." The questioner then wanted to know how he had been able to look up so many numbers from the tables so quickly. "Look them up?" Gauss responded. "Who needs to look them up? I just calculate them in my head!" In 1818 Gauss, putting his calculation skills to practical use, carried out a geodesic survey of the state of Hanover, linking up with previous Danish surveys. To aid in the survey, Gauss invented the heliotrope, an instrument that uses a mirror to reflect sunlight over great distances, to measure positions.

Gauss also claimed to have discovered the possibility of non-Euclidean geometries but never published it. This discovery was a major paradigm shift in mathematics, as it freed mathematicians from the mistaken belief that Euclid's axioms were the only way to make geometry consistent and non-contradictory. Research on these geometries led to, among other things, Einstein's theory of general relativity, which describes the universe as non-Euclidean. His friend Farkas Wolfgang Bolyai with whom Gauss had sworn "brotherhood and the banner of truth" as a student had tried in vain for many years to prove the parallel postulate from Euclid's other axioms of geometry. Bolyai's son, János Bolyai, discovered non-Euclidean geometry in 1829; his work was published in 1832. After seeing it, Gauss wrote to Farkas Bolyai: "To praise it would amount to praising myself. For the entire content of the work... coincides almost exactly with my own meditations which have occupied my mind for the past thirty or thirty-five years." This unproved statement put a strain on his relationship with János Bolyai (who thought that Gauss was "stealing" his idea), but it is now generally taken at face value. Letters by Gauss years before 1829 reveal him obscurely discussing the problem of parallel lines. Waldo Dunnington, a life-long student of Gauss, successfully proves in Gauss, Titan of Science that Gauss was in fact in full possession of non-Euclidian geometry long before it was published by János, but that he refused to publish any of it because of his fear of controversy.

The survey of Hanover fueled Gauss's interest in differential geometry, a field of mathematics dealing with curves and surfaces. Among other things he came up with the notion of Gaussian curvature. This led in 1828 to an important theorem, the Theorema Egregium (remarkable theorem in Latin), establishing an important property of the notion of curvature. Informally, the theorem says that the curvature of a surface can be determined entirely by measuring angles and distances on the surface. That is, curvature does not depend on how the surface might be embedded in 3-dimensional space or 2-dimensional space.

In 1821, he was made a foreign member of the Royal Swedish Academy of Sciences.

In 1831 Gauss developed a fruitful collaboration with the physics professor Wilhelm Weber, leading to new knowledge in  magnetism (including finding a representation for the unit of magnetism in terms of mass, length and time) and the discovery of Kirchhoff's circuit laws in electricity. They constructed the first electromechanical telegraph in 1833, which connected the observatory with the institute for physics in Göttingen. Gauss ordered a magnetic observatory to be built in the garden of the observatory, and with Weber founded the magnetischer Verein (magnetic club in German), which supported measurements of earth's magnetic field in many regions of the world. He developed a method of measuring the horizontal intensity of the magnetic field which has been in use well into the second half of the 20th century and worked out the mathematical theory for separating the inner (core and crust) and outer (magnetospheric) sources of Earth's magnetic field.

Gauss died in Göttingen, Hannover (now part of Lower Saxony, Germany) in 1855 and is interred in the cemetery Albanifriedhoft here. Two individuals gave eulogies at his funeral, Gauss's son-in-law Heinrich Ewald and Wolfgang Sartorius von Waltershausen, who was Gauss's close friend and biographer. His brain was preserved and was studied by Rudolf Wagner who found its mass to be 1,492 grams and the cerebral area equal to 219,588 square millimeters (340.362 square inches). Highly developed convolutions were also found, which in the early 20th century was suggested as the explanation of his genius.

Gauss's personal life was overshadowed by the early death of his first wife, Johanna Osthoff, in 1809, soon followed by the death of one child, Louis. Gauss plunged into a depression from which he never fully recovered. He married again, to Johanna's best friend named Friederica Wilhelmine Waldeck but commonly known as Minna. When his second wife died in 1831 after a long illness, one of his daughters, Therese, took over the household and cared for Gauss until the end of his life. His mother lived in his house from 1817 until her death in 1839.

Gauss was an ardent perfectionist and a hard worker. He was never a prolific writer, refusing to publish works which he did not consider complete and above criticism. This was in keeping with his personal motto pauca sed matura ("few, but ripe"). His personal diaries indicate that he had made several important mathematical discoveries years or decades before his contemporaries published them. Mathematical historian Eric Temple Bell estimated that had Gauss timely published all of his discoveries, Gauss would have advanced mathematics by fifty years. Though he did take in a few students, Gauss was known to dislike teaching. It is said that he attended only a single scientific conference, which was in Berlin in 1828. However, several of his students became influential mathematicians, among them Richard Dedekind, Bernhard Riemann, and Friedrich Bessel. Before she died, Sophie Germain was recommended by Gauss to receive her honorary degree. Gauss usually declined to present the intuition behind his often very elegant proofs—he preferred them to appear "out of thin air" and erased all traces of how he discovered them. This is justified, if unsatisfactorily, by Gauss in his "Disquisitiones Arithmeticae", where he states that all analysis must be suppressed for sake of brevity.

Gauss supported monarchy and opposed Napoleon, whom he saw as an outgrowth of revolution.