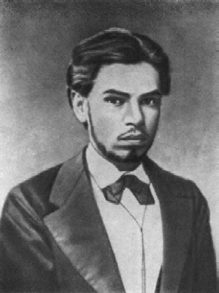
Aleksandr Mikhailovich Lyapunov (Russian: Александр Михайлович Ляпунов; June 6 [O.S. May 25] 1857 – November 3, 1918) was a Russian mathematician, mechanician and physicist. His surname is sometimes romanized as Ljapunov, Liapunov or Ljapunow. Lyapunov is known for his development of the stability theory of a dynamical system, as well as for his many contributions to mathematical physics and probability theory.

Lyapunov was born in Yaroslavl, Russian Empire. His father Mikhail Vasilyevich Lyapunov (1820 – 1868) was an astronomer and a head of the Demidovski lyceum. In 1863, M.V. Lyapunov retired from his scientific career and relocated his family to his wife's estate at Bolobonov, in the Simbirsk province (now Ulyanovsk Oblast). After the death of his father in 1868, Aleksandr Lyapunov was educated by his uncle R.M. Sechenov, brother of the famous physiologist Ivan Mikhailovich Sechenov. At his uncle's family, Lyapunov studied with his distant cousin Natalia Rafailovna, who became his wife in 1886. In 1870, his mother moved with her sons to Nizhny Novgorod, where he started the third class of the gymnasium. He graduated from the gymnasium with distinction in 1876.

In 1876 Lyapunov entered the Physico-Mathematical faculty of the University of Saint Petersburg, but after one month he transferred to the Mathematics department of the university. Among the Saint Petersburg professors of mathematics were Chebyshev and his students Aleksandr Nikolaevich Korkin and Yegor Ivanovich Zolotarev. Lyapunov wrote his first independent scientific works under the guidance of the professor of mechanics, D.K. Bobylev. In 1880 Lyapunov received a gold medal for a work on hydrostatics. This was the basis for his first published scientific works On the equilibrium of a heavy body in a heavy fluid contained in a vessel of a fixed form and On the potential of hydrostatic pressure. Lyapunov completed his university course in 1880, two years after Andrey Markov who had also graduated at Saint Petersburg University. Lyapunov would maintain a scientific contact with Markov during all his life.

In 1884 Lyapunov defended his Master's thesis On the stability of ellipsoidal forms of equilibrium of rotating fluids. This theme was suggested to him by Chebyshev, who had already suggested it to other students of his, such as Zolotarev and Sofia Vasilyevna Kovalevskaya. The thesis was publicized in 1885 in the Bulletin Astronomique. It was fully translated in French in 1904 and attracted the attention of mathematicians, physicists and astronomers in Europe.

In 1895 Lyapunov became privatdozent and was proposed to accept the chair of mechanics at Kharkiv University, where he went the same year. About the initial stay at Kharkiv, Lyapunov writes in his autobiography:

Here at first, the research activity of Lyapunov was cut short. It was necessary to work out courses and put together notes for students, which took up much time.

His student and collaborator, Vladimir Steklov, recalled his first lecture in the following way: "A handsome young man, almost of the age of the other students, came before the audience, where there was also the old Dean, professor Levakovsky, who was respected by all students. After the Dean had left, the young man with a trembled voice started to lecture a course on the dynamics of material points, instead of a course on dynamical systems. This subject was already known to the students from the lectures of professor Delarue. But what Lyapunov taught us was new to me and I had never seen this material in any textbook. All antipathy to the course was immediately blown to dust. From that day students would show Lyapunov a special respect."

In 1892 Lyapunov defended his famous doctoral thesis The general problem of the stability of motion. The thesis was defended in Moscow University on September 12, 1892, with Nikolai Zhukovsky and V.B. Mlodzeevski as opponents. This dissertation was, as with the master's, also translated into French. The next year Lyapunov became a full professor at Kharkiv University.

Lyapunov returned to Saint Petersburg in 1902, after being elected acting member of the Academy of Science as well as ordinary professor in the Faculty of Applied Mathematics of the university. The position had been left vacant by the death of his former teacher, Chebyshev. Not having any teaching obligations, this allowed Lyapunov to focus on his studies and in particular he was able to bring to a conclusion the work on the problem of Chebyshev with which he started his scientific career.

In 1908 he took part to the Fourth International Mathematical Congress in Rome. He also participated in the publication of Euler's selected works: he was an editor of the volumes 18 and 19.

By the end of June 1917, Lyapunov traveled with his wife to his brother's place in Odessa. Lyapunov's wife was suffering from tuberculosis so they moved following her doctor's orders. She died on October 31, 1918. The same day, Lyapunov shot himself in the head, and three days later he died.

Lyapunov contributed to several fields, including differential equations, potential theory, dynamical systems and probability theory. His main preoccupations were the stability of equilibria and the motion of mechanical systems, the model theory for the stability of uniform turbulent liquid, and the study of particles under the influence of gravity. His work in the field of mathematical physics regarded the boundary value problem of the equation of Laplace. In the theory of potential, his work from 1897 On some questions connected with Dirichlet's problem clarified several important aspects of the theory. His work in this field is in close connection with the work of Steklov. Lyapunov developed many important approximation methods. His methods, which he developed in 1899, make it possible to define the stability of sets of ordinary differential equations. He created the modern theory of the stability of a dynamic system. In the theory of probability, he generalised the works of Chebyshev and Markov, and proved the Central Limit Theorem under more general conditions than his predecessors. The method he used for the proof found later widespread use in probability theory.

Like many mathematicians, Lyapunov preferred to work alone and communicated mainly with few colleagues and close relatives. He usually worked late, four to five hours at night, sometimes the whole night. Once or twice a year he visited the theatre, or went to some concert. He had many students. He was an honorary member of many universities, an honorary member of the Academy in Rome and a corresponding member of the Academy of Sciences in Paris.