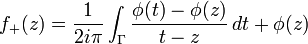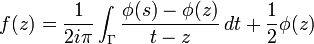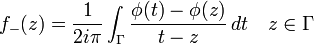Josip Plemelj (December 11, 1873 – May 22, 1967) was a Slovene mathematician.

Plemelj was born in the village of Grad on Bled (Grad na Bledu), Austria - Hungary (now Slovenia). He died in Ljubljana, Yugoslavia (now Slovenia). His father, Urban, a carpenter and crofter, died when Josip was only a year old. His mother Marija, née Mrak, found bringing up the family alone very hard, but she was able to send her son to school in Ljubljana where Plemelj studied from 1886 to 1894. After leaving and obtaining the necessary examination results he went to Vienna in 1894 where he had applied to the Faculty of Arts to study mathematics, physics and astronomy. His professors in Vienna were von Escherich for mathematical analysis, Gegenbauer and Mertens for arithmetic and algebra, Weiss for astronomy, Stefan's student Boltzmann for physics.

On May 1898 Plemelj presented his doctoral thesis under Escherich's tutelage entitled O linearnih homogenih diferencialnih enačbah z enolično periodičnimi koeficienti (Über lineare homogene Differentialgleichungen mit eindeutigen periodischen Koeffizienten, About linear homogeneous differential equations with uniform periodical coefficients). He continued with his study in Berlin (1899 - 1900) under the German mathematicians Frobenius and Fuchs and in Göttingen (1900 - 1901) under Klein and Hilbert.

In April 1902 he became a private senior lecturer at the University of Vienna. In 1906 he was appointed assistant at the Technical University of Vienna. In 1907 he became associate professor and in 1908 full professor of mathematics at the University of Chernivtsi (Russian Черновцы), Ukraine. From 1912 to 1913 he was dean of this faculty. In 1917 his political views led him to be forcibly ejected by the Government and he fled to Bohemia (Moravska). After the First World War he became a member of the University Commission under the Slovene Provincial Government and helped establish the first Slovene university at Ljubljana, and was elected its first rector. In the same year he was appointed professor of mathematics at the Faculty of Arts. After the Second World War he joined the Faculty of Natural Science and Technology (FNT). He retired in 1957 after having lectured in mathematics for 40 years.

Plemelj had shown his great gift for mathematics early in elementary school. He mastered the whole of the high school syllabus by the beginning of the fourth year and began to tutor students for their graduation examinations. At that time he discovered alone series for sin x and cos x. Actually he found a series for cyclometric function arccos x and after that he just inverted this series and then guessed a principle for coefficients. Yet he did not have a proof for that.

Plemelj had great joy for difficult constructional tasks from geometry. From his high school days originates an elementary problem — his later construction of regular sevenfold polygon inscribed in a circle otherwise exactly and not approximately with simple solution as an angle trisection which was yet not known in those days and which necessarily leads to the old Indian or Babylonian approximate construction. He started to occupy himself with mathematics in the fourth and fifth class of high school. Besides mathematics, he was interested also in natural science and especially astronomy. He studied celestial mechanics already at high school. He liked observing the stars.

His main research fields were (linear) differential equations, integral equations, potential theory (of harmonic functions), theory of analytical functions and function theory. When he was studying at Göttingen, Holmgren had reported about a theory which was developed by Fredholm for linear integral equations of the 1st and the 2nd degree. Mathematicians from Göttingen began to work on this new research field under Hilbert's guidance. Plemelj was among the first who had done a beginning work and he had achieved fine results. He had used integral equations in potential theory successfully.

His most important work in potential theory is a book entitled Raziskave v teoriji potenciala (Potentialtheoretische Untersuchungen, Researches in potential theory), "Preisschriften der fürstl. Jablonowskischen Gesselschaft in Leipzig", (Leipzig 1911) which in 1911 received an award from the Scientific society of prince Jablonowski in Leipzig in the amount of 1500 marks and the Richard Lieben award from the University of Vienna in the amount of 2000 crowns. The justification for for this award was that this work was the most outstanding on the field of pure and applied mathematics which had been written by any kind of 'Austrian' mathematician in the last three years.

His most important work in general is his original, marvellous and simple solution of the Riemann problem f₊=g f₋ about the existence of a differential equation with given monodromy group. He published his solution in 1908 in a treatise entitled Riemannovi razredi funkcij z dano monodromijsko grupo (Riemannsche Funktionenscharen mit gegebener Monodromiegruppe, Riemannian classes of functions with given monodromy group), "Monatshefte für Mathematik und Physik" 19, W 1908, 211 – 246. In solving the Riemann problem Plemelj used equations about boundary values of holomorphic functions which he had discovered a short time before and which are now called after him Plemelj formulae, Sokhotsky - Plemelj or sometimes (mainly in German literature) Plemelj - Sokhotsky formulae after the Russian mathematician Sokhotsky (Юлиан Карл Васильевич Сохоцкий ) (1842 – 1927):

From his method on solving the Riemann problem derived the theory of singular integral equations, which was developed above all by the Russian school headed by Muskhelishvili (Николай Иванович Мусхелищвили) (1891 – 1976).

Also important are Plemelj's contributions to the theory of analytic functions in solving the problem of uniformization of algebraic functions, contributions on formulation of the theorem of analytic extension of designs and treatises in algebra and in number theory.

In 1912 Plemelj published a very simple proof for the Fermat's last theorem for exponent n = 5, which was first given almost simultaneously by Dirichlet in 1828 and Legendre in 1830. Their proofs are difficult, while Plemelj showed how to use the ring we get if we extend the rational numbers by √ 5.

His arrival in Ljubljana 1919 was very important for development of mathematics in Slovenia. As a good teacher he had taught several generations of mathematicians and engineers. His most famous student is Ivan Vidav. After the 2nd World War Slovenska akademija znanosti in umetnosti (Slovene Academy of Sciences and Arts) (SAZU) had published his three year's course of lectures for students of mathematics: Teorija analitičnih funkcij (The theory of analytic functions), (SAZU, Ljubljana 1953), Diferencialne in integralske enačbe. Teorija in uporaba (Differential and integral equations. The theory and the application).

Plemelj found a formula for a sum of normal derivatives of one layered potential in the internal or external region. He worked also in algebra and number theory, but he had published only few contributions in these fields — for example a book entitled Algebra in teorija števil (Algebra and the number theory) (SAZU, Ljubljana 1962) which was published abroad as his last work Problemi v smislu Riemanna in Kleina (Problems in the Sense of Riemann and Klein) (edition and translation by J.R.M. Radok, "Interscience Tract in Pure and Applied Mathematics", No. 16, Interscience Publishers: John Wiley & Sons). His bibliography includes 33 units, from which 30 are scientific treatises and had been published in journals. 

Plemelj was regular member of the SAZU since its foundation in 1938, corresponding member of the JAZU (Yugoslav Academy of Sciences and Arts) in Zagreb, Croatia since 1923, corresponding member of the SANU (Serbian Academy of Sciences and Arts) in Belgrade since 1930 (1931). In 1954 he received the highest award for research in Slovenia, the Prešeren award. The same year he was elected as corresponding member of the Bavarian Academy of Sciences in Munich.

In 1963 for his 90th anniversary, the University of Ljubljana granted him an honorary doctor degree. Plemelj was the first teacher of mathematics at a Slovene university and in 1949 became first honorary member of ZDMFAJ, (Yugoslav Union of societies of mathematicians, physicists and astronomers). He left his villa in Bled to the DMFA where today is his memorial room.

Plemelj did not do extra preparation for lectures; he did not have any notes. He used to say that he thought over the lecture subject on the way from his home in Gradišče to the University. Students had the impression that he was creating the teaching material on the spot and that they were witnessing the formation of something new. He was writing formulae on the board beautifully although they were composited from Greek, Latin or Gothic letters. He demanded the same from the students.

Plemelj is said to have had a very refined ear for language and he had contributed a solid basis for the development of the Slovene mathematical terminology. He had accustomed students to using precise language and above all clear and logical phraseology. For example, he would become angry if they used the word 'rabiti' (to use) instead of the word 'potrebovati' (to need). To explain he said: "The engineer who does not know mathematics never needs it. But if he knows it, he uses it frequently".