<Back to Index>
- Mathematician Evert Willem Beth, 1908
- Writer Ludwig Ganghofer, 1855
- General of the U.S. Air Force Earle Everard "Pat" Partridge, 1900
PAGE SPONSOR
Evert Willem Beth (July 7, 1908 – April 12, 1964) was a Dutch philosopher and logician, whose work principally concerned the foundations of mathematics.
Beth was born in Almelo, a small town in the eastern Netherlands. His father had studied mathematics and physics at the University of Amsterdam, where he had been awarded a Ph.D.. Evert Beth studied the same subjects at Utrecht University, but then also studied philosophy and psychology. His 1935 Ph.D. was in philosophy.
In 1946, he became professor of logic and the foundations of mathematics in Amsterdam. Apart from two brief interruptions – a stint in 1951 as a research assistant to Alfred Tarski, and in 1957 as a visiting professor at Johns Hopkins University – he held the post in Amsterdam continuously until his death in 1964. His was the first academic post in his country in logic and the foundations of mathematics, and during this time he contributed actively to international cooperation in establishing logic as an academic discipline.
The
definition theorem states that a predicate (or function or constant) is
implicitly definable if and only if it is explicitly definable. A proof method for formal systems; cf. Gentzen's natural deduction and sequent calculus, or even J. Alan Robinson's resolution and Hilbert's axiomatic
systems. It is considered by many to be intuitively simple,
particularly for students not acquainted with the study of logic (Wilfrid Hodges for example presents semantic tableaux in his introductory textbook, Logic, and Melvin Fitting does the same in his presentation of first-order logic for computer scientists, First-order logic and automated theorem proving). One starts out with the intention of proving that a certain set
Beth Models are a class of relational models for non-classical logic (cf. Kripke semantics).
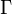of formulae imply another formula 
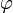, given a set of rules determined by the semantics of the formulae's connectives (and quantifiers, in First-order logic). The method is to assume the concurrent truth of every member of 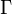and of 
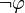(the negation of ),
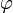and then to apply the rules to branch this list into a tree-like
structure of (simpler) formulae until every possible branch contains a
contradiction. At this point it will have been established that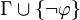 
is inconsistent, and thus that the formulae of 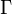together imply .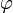