Alexander Gelfond was born in St Petersburg, Russian Empire, into the family of professional physician and amateur philosopher Osip Isaakovich Gelfond. He entered the Moscow State University in 1924, started his postgraduate studies there in 1927 and obtained his PhD in 1930. His advisors were Alexander Khinchin and Vyacheslav Stepanov.

In 1930 he stayed for five months in Germany (in Berlin and Göttingen) where he worked with Edmund Landau, Carl Ludwig Siegel and David Hilbert. In 1931 he started teaching as a Professor at the Moscow State University and worked there until the last day of his life. Since 1933 he also worked at the Steklov Institute of Mathematics.

In 1939 he was elected a Corresponding member of the Academy of Sciences of the USSR for his works in the field of Cryptography. During World War II he was the Chief Cryptographer of the Soviet Navy.

Gelfond obtained important results in several mathematical domains includinng number theory, analytic functions, integral equations and the history of mathematics, but his most famous result is his eponymous theorem:

If α and β are algebraic numbers (with α≠0 and α≠1), and if β is not a real rational number, then any value of α^β is a transcendental number.

This is the famous 7th Hilbert's problem. Gelfond proved a special case of the theorem in 1929, when he was a postgraduate student and fully proved it in 1934. In 1935 the same theorem was independently proved by Theodor Schneider and so the theorem is often known as the Gelfond – Schneider theorem. In 1929 Gelfond proposed an extension of the theorem known as the Gelfond's conjecture that was proved by Alan Baker in 1966.

Before Gelfond's works only a few numbers such as e and π were known to be transcendental. After his works an infinite number of transcendentals could be easily obtained. Some of them are named in Gelfond's honor: 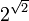 is known as the Gelfond – Schneider constant;  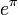is known as Gelfond's constant.