Abū Kāmil, Shujāʿ ibn Aslam ibn Muḥammad Ibn Shujāʿ (Latinized as Auoquamel, Arabic: ابو كامل‎, also known as al-ḥāsib al-miṣrī — literally, "the Egyptian calculator") (c. 850 – c. 930) was an Egyptian Muslim mathematician during the Islamic Golden Age. He made important contributions to algebra and geometry, and considered the first mathematician to systematically use and accept irrational numbers as solutions and coefficients to equations. His mathematical techniques were later adopted by Fibonacci, thus allowing Abu Kamil an important part in introducing algebra to Europe.

He was also the first Islamic mathematician to work easily with algebraic equations with powers higher than x² (up to x⁸), and solved sets of non - linear simultaneous equations with three unknown variables. He wrote all problems rhetorically, and some of his books lacked any mathematical notation beside those of integers. For example, he uses the Arabic expression "māl māl shayʾ" ("square - square - thing") for x⁵ (i.e., ).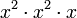

Known as Kitāb fi al-jabr wa al-muqābala, perhaps Abu Kamil's most influential work, intended to supersede and expand upon that of Al-Khawarizmi. Whereas the Algebra of al-Khawarizmi was intended towards the general public, Abu Kamil was addressing other mathematicians, or readers familiar with Euclid's Elements. In this work Abu Kamil solved systems of equations whose solutions are whole numbers and fractions, and accepted irrational numbers (in the form of a square root or fourth root) as solutions and coefficients to quadratic equations.

The first chapter teaches algebra by solving problems of application to geometry, often involving an unknown variable and square roots. The second chapter deals with the six types of problems found in Al-Khawarizmi's book, but some of which, especially those of x², was now worked out directly instead of first solving for x, and accompanied with geometrical illustrations and proofs. The third chapter contains examples of quadratic irrationalities as solutions and coefficients. In the fourth chapter, these irrationalities are used to solve problems involving polygons. The rest of the book contains sets of indeterminate equations and systems, problems of application in realistic situations, and problems involving unrealistic situations intended for recreational mathematics.

A number of Islamic mathematicians wrote commentaries on this work, including al-Iṣṭakhrī al-Ḥāsib and ʿAli ibn Aḥmad al-ʿImrānī (d. 955-6), but both commentaries are lost. In Europe, similar material to this book is found in the writings of Fibonacci, and some sections were incorporated and improved upon in the Latin work of John of Seville, Liber mahameleth. A partial translation to Latin was done in the 14th century by William of Luna, and in the 15th century the whole work also appeared in a Hebrew translation by Mordekhai Finzi.

Kitāb al-ṭarā’if fi’l-ḥisāb, describes a number of systematic procedures for finding integral solutions for indeterminate equations. It is the earliest known Arabic work where solutions are sought to the type of indeterminate equations found in Diophantus's Arithmetica. Abu Kamil explains certain methods not found in any extant copy of the Arithmetica. He also describes one problem for which he found 2,678 solutions.
Kitāb … al-mukhammas wa’al-mu‘ashshar. In this treatise algebraic methods are used to solve geometrical problems. Abu Kamil uses the equation x⁴ + 3125 = 125x² to calculate a numerical approximation for the side of a regular pentagon in a circle of radius 10. He also uses the Golden Ratio in some of his calculations. Fibonacci knew about this treatise and made extensive use of it in his Practica geometriae.

Kitāb al-ṭair, a small treatise teaching how to solve indeterminate linear systems with positive integral solutions. The title is derived from a type of problems known in the east which involve the purchase of different species of birds. Abu Kamil wrote in the introduction:

I found myself before a problem that I solved and for which I discovered a great many solutions; looking deeper for its solutions, I obtained two thousand six hundred and seventy - six correct ones. My astonishment about that was great, but I found out that, when I recounted this discovery, those who did not know me were arrogant, shocked, and suspicious of me. I thus decided to write a book on this kind of calculations, with the purpose of facilitating its treatment and making it more accessible.

According to Jacques Sesiano, Abu Kamil remained seemingly unparalleled throughout the Middle Ages in trying to find all the possible solutions to some of his problems.

Kitāb al-misāḥa wa al-handasa, a manual of geometry for non - mathematicians, like land surveyors and other government officials. It presents a set rules for calculating the volume and surface area of solids (mainly rectangular parallelepipeds, right circular prisms, square pyramids, and circular cones). Its first few chapters also contain rules for determining the area, diagonal, perimeter, etc, of different types of triangles, rectangles and squares.

Abu Kamil wrote a now lost treatise on the use of double false position, known as the Book of the Two Errors (Kitāb al-khaṭaʾayn).

Another lost work of his is the Book on Augmentation and Diminution (Kitāb al-jamʿ wa al-tafrīq), which gained more attention after historian Franz Woepcke linked it with another Latin work, Liber augmenti et diminutionis.

He also wrote the Book of Estate Sharing using Algebra (Kitāb al-waṣāyā bi al-jabr wa al-muqābala), which contains algebraic solutions for problems of Islamic inheritance and discusses the opinions of known jurists.

Ibn al-Nadīm in his Fihrist listed the following additional titles: Book of Fortune (Kitāb al-falāḥ), Book of the Key to Fortune (Kitāb miftāḥ al-falāḥ), Book of the Adequate (Kitāb al-kifāya), and Book of the Kernel (Kitāb al-ʿasīr).

The works of Abu Kamil influenced other mathematicians, like al-Karaji and Fibonacci, and as such had a lasting impact on the development of algebra. Many of his examples and algebraic techniques were later copied by Fibonacci in his Practica geometriae and other works. Unmistakable borrowings, but without Abu Kamil being explicitly mentioned and perhaps mediated by lost treatises, are also found in Fibonacci's Liber Abaci.

Almost nothing is known about the life and career of Abu Kamil except that he was a successor of al-Khawarizmi, whom he never personally met. He was also one of the earliest mathematicians to recognize Al-Khwarizmi's contributions to algebra, and defended him against Ibn Barza who attributed the authority and precedent in algebra to his grandfather, ʿAbd al-Hamīd ibn Turk.

Abu Kamil wrote in the introduction of his Algebra:

I have studied with great attention the writings of the mathematicians, examined their assertions, and scrutinized what they explain in their works; I thus observed that the book by Muḥammad ibn Mūsā al-Khawārizmī known as Algebra is superior in the accuracy of its principle and the exactness of its argumentation. It thus behooves us, the community of mathematicians, to recognize his priority and to admit his knowledge and his superiority, as in writing his book on algebra he was an initiator and the discoverer of its principles, ...