Pythagoras of Samos (Ancient Greek: Ὁ Πυθαγόρας ὁ Σάμιος "Pythagoras the Samian", or simply Ὁ Πυθαγόρας; c. 570 – c. 495 BC) was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him. He was born on the island of Samos, and might have traveled widely in his youth, visiting Egypt and other places seeking knowledge. He had a teacher named Themistocles, who introduced him to the principles of ethics. Around 530 BC, he moved to Croton, a Greek colony in southern Italy, and there set up a religious sect. His followers pursued the religious rites and practices developed by Pythagoras, and studied his philosophical theories. The society took an active role in the politics of Croton, but this eventually led to their downfall. The Pythagorean meeting places were burned, and Pythagoras was forced to flee the city. He is said to have ended his days in Metapontum.

Pythagoras made influential contributions to philosophy and religious teaching in the late 6th century BC. He is often revered as a great mathematician, mystic and scientist, but he is best known for the Pythagorean theorem which bears his name. However, because legend and obfuscation cloud his work even more than with the other pre - Socratic philosophers, one can give account of his teachings to a little extent, and some have questioned whether he contributed much to mathematics and natural philosophy. Many of the accomplishments credited to Pythagoras may actually have been accomplishments of his colleagues and successors. Whether or not his disciples believed that everything was related to mathematics and that numbers were the ultimate reality is unknown. It was said that he was the first man to call himself a philosopher, or lover of wisdom, and Pythagorean ideas exercised a marked influence on Plato, and through him, all of Western philosophy.

Accurate facts about the life of Pythagoras are so few, and most information concerning him is of so late a date, and so untrustworthy, that it is impossible to provide more than a vague outline of his life. The lack of information by contemporary writers, together with the secrecy which surrounded the Pythagorean brotherhood, meant that invention took the place of facts. The stories which were created were eagerly sought by the Neoplatonist writers who provide most of the details about Pythagoras, but who were uncritical concerning anything which related to the gods or which was considered divine. Thus many myths were created – such as that Apollo was his father; that Pythagoras gleamed with a supernatural brightness; that he had a golden thigh; that Abaris came flying to him on a golden arrow; that he was seen in different places at one and the same time. With the exception of a few remarks by Xenophanes, Heraclitus, Herodotus, Plato, Aristotle, and Isocrates, we are mainly dependent on Diogenes Laërtius, Porphyry, and Iamblichus for the biographical details. Aristotle had written a separate work on the Pythagoreans, which unfortunately has not survived. His disciples Dicaearchus, Aristoxenus, and Heraclides Ponticus had written on the same subject. These writers, late as they are, were among the best sources from whom Porphyry and Iamblichus drew, besides the legendary accounts and their own inventions. Hence historians are often reduced to considering the statements based on their inherent probability, but even then, if all the credible stories concerning Pythagoras were supposed true, his range of activity would be impossibly vast.

Herodotus, Isocrates, and other early writers all agree that Pythagoras was born on Samos, the Greek island in the eastern Aegean, and we also learn that Pythagoras was the son of Mnesarchus. His father was a gem engraver or a merchant. His name led him to be associated with Pythian Apollo; Aristippus explained his name by saying, "He spoke (agor-) the truth no less than did the Pythian (Pyth-)," and Iamblichus tells the story that the Pythia prophesied that his pregnant mother would give birth to a man supremely beautiful, wise, and beneficial to humankind. A late source gives his mother's name as Pythais. As to the date of his birth, Aristoxenus stated that Pythagoras left Samos in the reign of Polycrates, at the age of 40, which would give a date of birth around 570 BC.

It was natural for the ancient biographers to inquire as to the origins of Pythagoras' remarkable system. In the absence of reliable information, however, a huge range of teachers were assigned to Pythagoras. Some made his training almost entirely Greek, others exclusively Egyptian and Oriental. We find mentioned as his instructors Creophylus, Hermodamas, Bias, Thales, Anaximander, and Pherecydes of Syros. The Egyptians are said to have taught him geometry, the Phoenicians arithmetic, the Chaldeans astronomy, the Magians the principles of religion and practical maxims for the conduct of life. Of the various claims regarding his Greek teachers, Pherecydes is mentioned most often.

Diogenes Laertius reported that Pythagoras had undertaken extensive travels, and had visited not only Egypt, but Arabia, Phoenicia, Judaea, Babylon, and even India, for the purpose of collecting all available knowledge, and especially to learn information concerning the secret or mystic cults of the gods. Plutarch asserted in his book On Isis and Osiris that during his visit to Egypt, Pythagoras received instruction from the Egyptian priest Oenuphis of Heliopolis. Other ancient writers asserted his visit to Egypt. Enough of Egypt was known to attract the curiosity of an inquiring Greek, and contact between Samos and other parts of Greece with Egypt is mentioned.

It is not easy to say how much Pythagoras learned from the Egyptian priests, or indeed, whether he learned anything at all from them. There was nothing in the symbolism which the Pythagoreans adopted which showed the distinct traces of Egypt. The secret religious rites of the Pythagoreans exhibited nothing but what might have been adopted in the spirit of Greek religion, by those who knew nothing of Egyptian mysteries. The philosophy and the institutions of Pythagoras might easily have been developed by a Greek mind exposed to the ordinary influences of the age. Even the ancient authorities note the similarities between the religious and ascetic peculiarities of Pythagoras with the Orphic or Cretan mysteries, or the Delphic oracle.

There is little direct evidence as to the kind and amount of knowledge which Pythagoras acquired, or as to his definite philosophical views. Everything of the kind mentioned by Plato and Aristotle is attributed not to Pythagoras, but to the Pythagoreans. Heraclitus stated that he was a man of extensive learning; and Xenophanes claimed that he believed in the transmigration of souls. Xenophanes mentions the story of his interceding on behalf of a dog that was being beaten, professing to recognize in its cries the voice of a departed friend. Pythagoras is supposed to have claimed that he had been Euphorbus, the son of Panthus, in the Trojan war, as well as various other characters, a tradesman, a courtesan, etc. In his book The Life of Apollonius of Tyana, Philostratus wrote that Pythagoras knew not only who he was himself, but also who he had been.

Many mathematical and scientific discoveries were attributed to Pythagoras, including his famous theorem, as well as discoveries in the field of music, astronomy, and medicine. But it was the religious element which made the profoundest impression upon his contemporaries. Thus the people of Croton were supposed to have identified him with the Hyperborean Apollo, and he was said to have practiced divination and prophecy. In the visits to various places in Greece – Delos, Sparta, Phlius, Crete, etc. which are ascribed to him, he usually appears either in his religious or priestly guise, or else as a law giver.

After his travels, Pythagoras moved (around 530 BC) to Croton, in Italy (Magna Graecia). Possibly the tyranny of Polycrates in Samos made it difficult for him to achieve his schemes there. His later admirers claimed that Pythagoras was so overburdened with public duties in Samos, because of the high estimation in which he was held by his fellow citizens, that he moved to Croton. On his arrival in Croton, he quickly attained extensive influence, and many people began to follow him. Later biographers tell fantastical stories of the effects of his eloquent speech in leading the people of Croton to abandon their luxurious and corrupt way of life and devote themselves to the purer system which he came to introduce.

His followers established a select brotherhood or club for the purpose of pursuing the religious and ascetic practices developed by their master. The accounts agree that what was done and taught among the members was kept a profound secret. The esoteric teachings may have concerned the secret religious doctrines and usages, which were undoubtedly prominent in the Pythagorean system, and may have been connected with the worship of Apollo. Temperance of all kinds seems to have been strictly urged. There is disagreement among the biographers as to whether Pythagoras forbade all animal food, or only certain types. The club was in practice at once "a philosophical school, a religious brotherhood, and a political association."

Such an aristocratic and exclusive club could easily have made many people in Croton jealous and hostile, and this seems to have led to its destruction. The circumstances, however, are uncertain. Conflict seems to have broken out between the towns of Sybaris and Croton. The forces of Croton were headed by the Pythagorean Milo, and it is likely that the members of the brotherhood took a prominent part. After the decisive victory by Croton, a proposal for establishing a more democratic constitution, was unsuccessfully resisted by the Pythagoreans. Their enemies, headed by Cylon and Ninon, the former of whom is said to have been irritated by his exclusion from the brotherhood, roused the populace against them. An attack was made upon them while assembled either in the house of Milo, or in some other meeting place. The building was set on fire, and many of the assembled members perished; only the younger and more active escaping. Similar commotions ensued in the other cities of Magna Graecia in which Pythagorean clubs had been formed.

As an active and organized brotherhood the Pythagorean order was everywhere suppressed, and did not again revive. Still the Pythagoreans continued to exist as a sect, the members of which kept up among themselves their religious observances and scientific pursuits, while individuals, as in the case of Archytas, acquired now and then great political influence. Concerning the fate of Pythagoras himself, the accounts varied. Some say that he perished in the temple with his disciples, others that he fled first to Tarentum, and that, being driven from there, he escaped to Metapontum, and there starved himself to death. His tomb was shown at Metapontum in the time of Cicero.

According to some accounts Pythagoras married Theano, a lady of Croton. Their children are variously stated to have included a son, Telauges, and three daughters, Damo, Arignote, and Myia.

No texts by Pythagoras are known to have survived, although forgeries under his name — a few of which remain extant — did circulate in antiquity. Critical ancient sources like Aristotle and Aristoxenus cast doubt on these writings. Ancient Pythagoreans usually quoted their master's doctrines with the phrase autos ephe ("he himself said") — emphasizing the essentially oral nature of his teaching.

Since the fourth century AD, Pythagoras has commonly been given credit for discovering the Pythagorean theorem, a theorem in geometry that states that in a right - angled triangle the area of the square on the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares of the other two sides — that is, a² + b² = c².

While the theorem that now bears his name was known and previously utilized by the Babylonians and Indians, he, or his students, are often said to have constructed the first proof. It must, however, be stressed that the way in which the Babylonians handled Pythagorean numbers implies that they knew that the principle was generally applicable, and knew some kind of proof, which has not yet been found in the (still largely unpublished) cuneiform sources. Because of the secretive nature of his school and the custom of its students to attribute everything to their teacher, there is no evidence that Pythagoras himself worked on or proved this theorem. For that matter, there is no evidence that he worked on any mathematical or meta - mathematical problems. Some attribute it as a carefully constructed myth by followers of Plato over two centuries after the death of Pythagoras, mainly to bolster the case for Platonic meta - physics, which resonate well with the ideas they attributed to Pythagoras. This attribution has stuck down the centuries up to modern times. The earliest known mention of Pythagoras's name in connection with the theorem occurred five centuries after his death, in the writings of Cicero and Plutarch.

According to legend, the way Pythagoras discovered that musical notes could be translated into mathematical equations was when one day he passed blacksmiths at work, and thought that the sounds emanating from their anvils being hit were beautiful and harmonious and decided that whatever scientific law caused this to happen must be mathematical and could be applied to music. He went to the blacksmiths to learn how this had happened by looking at their tools, he discovered that it was because the hammers were "simple ratios of each other, one was half the size of the first, another was 2/3 the size, and so on."

This legend has since proven to be false by virtue of the fact that these ratios are only relevant to string length (such as the string of a monochord), and not to hammer weight. However, it may be that Pythagoras was indeed responsible for discovering these properties of string length.

Pythagoreans elaborated on a theory of numbers, the exact meaning of which is still debated among scholars. Another belief attributed to Pythagoras was that of the "harmony of the spheres". Thus the planets and stars moved according to mathematical equations, which corresponded to musical notes and thus produced a symphony.

Pythagoras was also credited with devising the tetractys, the triangular figure of four rows, which add up to the perfect number, ten. As a mystical symbol, it was very important to the worship of the Pythagoreans, who would swear oaths by it:

And the inventions were so admirable, and so divinized by those who understood them, that the members used them as forms of oath: "By him who handed to our generation the tetractys, source of the roots of ever - flowing nature."

—Iamblichus, Vit. Pyth., 29

Pythagoras became the subject of elaborate legends surrounding his historic persona. Aristotle described Pythagoras as a wonder - worker and somewhat of a supernatural figure, attributing to him such aspects as a golden thigh, which was a sign of divinity. According to Muslim tradition, Pythagoras was said to have been initiated by Hermes (Egyptian Thoth). According to Aristotle and others' accounts, some ancients believed that he had the ability to travel through space and time, and to communicate with animals and plants. An extract from Brewer's Dictionary of Phrase and Fable's entry entitled "Golden Thigh":

Pythagoras is said to have had a golden thigh, which he showed to Abaris, the Hyperborean priest, and exhibited in the Olympic games.

Another legend describes his writing on the moon:

Pythagoras asserted he could write on the moon. His plan of operation was to write on a looking - glass in blood, and place it opposite the moon, when the inscription would appear photographed or reflected on the moon's disc.

Both Plato and Isocrates affirm that, above all else, Pythagoras was famous for leaving behind him a way of life. Both Iamblichus and Porphyry give detailed accounts of the organization of the school, although the primary interest of both writers is not historical accuracy, but rather to present Pythagoras as a divine figure, sent by the gods to benefit humankind.

Pythagoras set up an organization which was in some ways a school, in some ways a brotherhood (and here it should be noted that sources indicate that as well as men there were many women among the adherents of Pythagoras), and in some ways a monastery. It was based upon the religious teachings of Pythagoras and was very secretive. The adherents were bound by a vow to Pythagoras and each other, for the purpose of pursuing the religious and ascetic observances, and of studying his religious and philosophical theories. The claim that they put all their property into a common stock is perhaps only a later inference from certain Pythagorean maxims and practices.

As to the internal arrangements of the sect, we are informed that what was done and taught among the members was kept a profound secret towards all. Porphyry stated that this silence was "of no ordinary kind." Candidates had to pass through a period of probation, in which their powers of maintaining silence (echemythia) were especially tested, as well as their general temper, disposition, and mental capacity. There were also gradations among the members themselves. It was an old Pythagorean maxim, that every thing was not to be told to every body. Thus the Pythagoreans were divided into an inner circle called the mathematikoi ("learners") and an outer circle called the akousmatikoi ("listeners"). Iamblichus describes them in terms of esoterikoi and exoterikoi (or alternatively Pythagoreioi and Pythagoristai), according to the degree of intimacy which they enjoyed with Pythagoras. Porphyry wrote "the mathematikoi learned the more detailed and exactly elaborated version of this knowledge, the akousmatikoi (were) those who had heard only the summary headings of his (Pythagoras's) writings, without the more exact exposition."

There were ascetic practices (many of which had, perhaps, a symbolic meaning) in the way of life of the sect. Some represent Pythagoras as forbidding all animal food, advocating a plant - based diet, and prohibiting consumption of beans. This may have been due to the doctrine of metempsychosis. Other authorities contradict the statement. According to Aristoxenus, he allowed the use of all kinds of animal food except the flesh of oxen used for ploughing, and rams. There is a similar discrepancy as to the prohibition of fish and beans. But temperance of all kinds seems to have been urged. It is also stated that they had common meals, resembling the Spartan system, at which they met in companies of ten.

Considerable importance seems to have been attached to music and gymnastics in the daily exercises of the disciples. Their whole discipline is represented as encouraging a lofty serenity and self - possession, of which, there were various anecdotes in antiquity. Iamblichus (apparently on the authority of Aristoxenus) gives a long description of the daily routine of the members, which suggests many similarities with Sparta. The members of the sect showed a devoted attachment to each other, to the exclusion of those who did not belong to their ranks. There were even stories of secret symbols, by which members of the sect could recognize each other, even if they had never met before.

Pythagoras, or in a broader sense, the Pythagoreans, allegedly exercised an important influence on the work of Plato. According to R. M. Hare, this influence consists of three points: (1) The platonic Republic might be related to the idea of "a tightly organized community of like minded thinkers", like the one established by Pythagoras in Croton. (2) There is evidence that Plato possibly took from Pythagoras the idea that mathematics and, generally speaking, abstract thinking is a secure basis for philosophical thinking as well as "for substantial theses in science and morals". (3) Plato and Pythagoras shared a "mystical approach to the soul and its place in the material world". It is probable that both were influenced by Orphism.

Aristotle claimed that the philosophy of Plato closely followed the teachings of the Pythagoreans, and Cicero repeats this claim: Platonem ferunt didicisse Pythagorea omnia ("They say Plato learned all things Pythagorean"). Bertrand Russell, in his A History of Western Philosophy, contended that the influence of Pythagoras on Plato and others was so great that he should be considered the most influential of all Western philosophers.

Pythagoras started a secret society called the Pythagorean brotherhood devoted to the study of mathematics. This had a great effect on future esoteric traditions, such as Rosicrucianism and Freemasonry, both of which were occult groups dedicated to the study of mathematics and both of which claimed to have evolved out of the Pythagorean brotherhood. The mystical and occult qualities of Pythagorean mathematics are discussed in a chapter of Manly P. Hall's The Secret Teachings of All Ages entitled "Pythagorean Mathematics". Pythagorean theory was tremendously influential on later numerology, which was extremely popular throughout the Middle East in the ancient world. The 8th century Muslim alchemist Jabir ibn Hayyan grounded his work in an elaborate numerology greatly influenced by Pythagorean theory. Today, Pythagoras is revered as a prophet by the Ahl al-Tawhid or Druze faith along with his fellow Greek, Plato.

Little is known about the life of Diophantus. He lived in Alexandria, Egypt, probably from between 200 and 214 to 284 or 298 AD. Much of our knowledge of the life of Diophantus is derived from a 5th century Greek anthology of number games and strategy puzzles. One of the problems (sometimes called his epitaph) states:

'Here lies Diophantus,' the wonder behold.

Through art algebraic, the stone tells how old:

'God gave him his boyhood one - sixth of his life,

One twelfth more as youth while whiskers grew rife;

And then yet one - seventh ere marriage begun;

In five years there came a bouncing new son.

Alas, the dear child of master and sage

After attaining half the measure of his father's life chill fate took him.

After consoling his fate by the science of numbers for four years, he ended his life.'

This puzzle implies that Diophantus lived to be 84 years old. However, the accuracy of the information cannot be independently confirmed.

In popular culture, this puzzle was the Puzzle No.142 in Professor Layton and Pandora's Box as one of the hardest solving puzzles in the game, which needed to be unlocked by solving other puzzles first.

The Arithmetica is the major work of Diophantus and the most prominent work on algebra in Greek mathematics. It is a collection of problems giving numerical solutions of both determinate and indeterminate equations. Of the original thirteen books of which Arithmetica consisted only six have survived, though there are some who believe that four Arab books discovered in 1968 are also by Diophantus. Some Diophantine problems from Arithmetica have been found in Arabic sources.

It should be mentioned here that Diophantus never used general methods in his solutions. Hermann Hankel, renowned German mathematician, made the following remark regarding Diophantus.

“Our author (Diophantos) not the slightest trace of a general, comprehensive method is discernible; each problem calls for some special method which refuses to work even for the most closely related problems. For this reason it is difficult for the modern scholar to solve the 101st problem even after having studied 100 of Diophantos’s solutions”.

Like many other Greek mathematical treatises, Diophantus was forgotten in Western Europe during the so-called Dark Ages, since the study of ancient Greek had greatly declined. The portion of the Greek Arithmetica that survived, however, was, like all ancient Greek texts transmitted to the early modern world, copied by, and thus known to, medieval Byzantine scholars. In addition, some portion of the Arithmetica probably survived in the Arab tradition. In 1463 German mathematician Regiomontanus wrote:

“No one has yet translated from the Greek into Latin the thirteen books of Diophantus, in which the very flower of the whole of arithmetic lies hidden . . . .”

Arithmetica was first translated from Greek into Latin by Bombelli in 1570, but the translation was never published. However, Bombelli borrowed many of the problems for his own book Algebra. The editio princeps of Arithmetica was published in 1575 by Xylander. The best known Latin translation of Arithmetica was made by Bachet in 1621 and became the first Latin edition that was widely available. Pierre de Fermat owned a copy, studied it, and made notes in the margins.

The 1621 edition of Arithmetica by Bachet gained fame after Pierre de Fermat wrote his famous "Last Theorem" in the margins of his copy:

“If an integer n is greater than 2, then aⁿ + bⁿ = cⁿ has no solutions in non-zero integers a, b, and c. I have a truly marvelous proof of this proposition which this margin is too narrow to contain.”

Fermat's proof was never found, and the problem of finding a proof for the theorem went unsolved for centuries. A proof was finally found in 1994 by Andrew Wiles after working on it for seven years. It is believed that Fermat did not actually have the proof he claimed to have. Although the original copy in which Fermat wrote this is lost today, Fermat's son edited the next edition of Diophantus, published in 1670. Even though the text is otherwise inferior to the 1621 edition, Fermat's annotations — including the "Last Theorem" — were printed in this version.

Fermat was not the first mathematician so moved to write in his own marginal notes to Diophantus; the Byzantine scholar John Chortasmenos (14th / 15th C.) had written "Thy soul, Diophantus, be with Satan because of the difficulty of your theorems" next to the same problem.

Diophantus wrote several other books besides Arithmetica, but very few of them have survived.

Diophantus himself refers to a work which consists of a collection of lemmas called The Porisms (or Porismata), but this book is entirely lost. Some scholars think that The porisms may have actually been a section of Arithmetica that is now lost.

Although The Porisms is lost, we know three lemmas contained there, since Diophantus refers to them in the Arithmetica. One lemma states that the difference of the cubes of two rational numbers is equal to the sum of the cubes of two other rational numbers, i.e. given any a and b, with a > b, there exist c and d, all positive and rational, such that

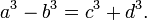
Diophantus is also known to have written on polygonal numbers, a topic of great interest to Pythagoras and Pythagoreans. Fragments of a book dealing with polygonal numbers are extant.

A book called Preliminaries to the Geometric Elements has been traditionally attributed to Hero of Alexandria. It has been studied recently by Wilbur Knorr, who suggested that the attribution to Hero is incorrect, and that the true author is Diophantus.

Diophantus made important advances in mathematical notation. He was the first person to use algebraic notation and symbolism. Before him everyone wrote out equations completely. Diophantus introduced an algebraic symbolism that used an abridged notation for frequently occurring operations, and an abbreviation for the unknown and for the powers of the unknown. Mathematical historian Kurt Vogel states:

“The symbolism that Diophantus introduced for the first time, and undoubtedly devised himself, provided a short and readily comprehensible means of expressing an equation... Since an abbreviation is also employed for the word ‘equals’, Diophantus took a fundamental step from verbal algebra towards symbolic algebra.”

Although Diophantus made important advances in symbolism, he still lacked the necessary notation to express more general methods. This caused his work to be more concerned with particular problems rather than general situations. Some of the limitations of Diophantus' notation are that he only had notation for one unknown and, when problems involved more than a single unknown, Diophantus was reduced to expressing "first unknown", "second unknown", etc. in words. He also lacked a symbol for a general number n. Where we would write(12 + 6n) / (n² − 3), Diophantus has to resort to constructions like : ... a sixfold number increased by twelve, which is divided by the difference by which the square of the number exceeds three.

Algebra still had a long way to go before very general problems could be written down and solved succinctly.