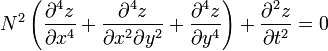Marie - Sophie Germain was born on April 1, 1776, in Paris, France, in a house on Rue Saint - Denis. According to most sources, her father, Ambroise - Franҫois, was a wealthy silk merchant. However, Dr. Mary Gray, the chairman of the Department of Mathematics and Statistics at American University in Washington, D.C., has said that he was a goldsmith. In 1789, he was elected as a representative of the bourgeoisie to the États - Généraux, which he saw change into the Constitutional Assembly. It is therefore assumed that Sophie witnessed many discussions between her father and his friends on politics and philosophy. Gray proposes that after his political career, Ambroise - Franҫois became the director of a bank; at least, the family remained well off enough to support Germain throughout her adult life.

Marie - Sophie had one younger sister, named Angélique - Ambroise, and one older sister, named Marie - Madeline. Her mother was also named Marie - Madeline, and this plethora of "Maries" may have been the reason she went by Sophie. Germain's nephew Armand - Jacques Lherbette, Marie - Madeline's son, published some of Germain's work after she died.

When Germain was 13, the Bastille fell, and the revolutionary atmosphere of the city forced her to stay inside. For entertainment she turned to her father's library. Here she found J.E. Montucla's L'Histoire des Mathématiques, and his story of the death of Archimedes intrigued her.

Germain decided that if geometry, which at that time referred to all of pure mathematics, could hold such fascination for Archimedes, it was a subject worthy of study. So she pored over every book on mathematics in her father's library, even teaching herself Latin and Greek so she could read works like those of Sir Isaac Newton and Leonhard Euler. She also enjoyed Traité d'Arithmétique by Étienne Bézout and Le Calcul Différential by Jacques Antoine - Joseph Cousin. Later, Cousin visited her in her house, encouraging her in her studies.

Germain's parents did not at all approve of her sudden fascination with mathematics, which was then thought inappropriate for a woman. When night came, they would deny her warm clothes and a fire for her bedroom to try to keep her from studying, but after they left she would take out candles, wrap herself in quilts and do mathematics. As UC Irvine's Women's Studies professor Lynn Osen describes, when her parents found Sophie “asleep at her desk in the morning, the ink frozen in the ink horn and her slate covered with calculations,” they realized that their daughter was serious and relented. After some time, her mother even secretly supported her.

In 1794, when Germain was 18, the École Polytechnique opened. As a woman, Germain was barred from attending, but the new system of education made the “lecture notes available to all who asked." The new method also required the students to “submit written observations." Germain obtained the lecture notes and began sending her work to Joseph Louis Lagrange, a faculty member. She used the name M. LeBlanc, “fearing,” as she later explained to Gauss, “the ridicule attached to a female scientist." When Lagrange saw the intelligence of M. LeBlanc, he requested a meeting, and thus Sophie was forced to disclose her true identity. Fortunately, Lagrange did not mind that Germain was a woman, and he became her mentor. He too visited her in her home, giving her moral support.

Germain first became interested in number theory in 1798 when Adrien - Marie Legendre published Essai sur la théorie des nombres. After studying the work, she opened correspondence with him on number theory, and later, elasticity. Legendre showed some of Germain's work in the Supplément to his second edition of the Théorie des Nombres, where he calls it très ingénieuse.

Germain's interest in number theory was renewed when she read Carl Friedrich Gauss' monumental work Disquisitiones Arithmeticae. After three years of working through the exercises and trying her own proofs for some of the theorems, she wrote, again under the pseudonym of M. LeBlanc, to the author himself, who was one year younger than she. The first letter, dated 21 November 1804, discussed Gauss' Disquisitiones and presented some of Germain's work on Fermat's Last Theorem. In the letter, Germain claimed to have proved the theorem for n = p – 1, where p is a prime number of the form p = 8k + 7; however, her proof contained a weak assumption. Gauss' reply did not comment on Germain's proof.

Around 1807 (sources differ), the French were occupying the German town of Braunschweig, where Gauss lived. Germain, concerned that he might suffer the fate of Archimedes, wrote to General Pernety, a family friend, requesting that he ensure Gauss' safety. General Pernety sent a chief of a battalion to meet with Gauss personally to see that he was safe. As it turned out, Gauss was fine, but he was confused by the mention of Sophie's name.

Three months after the incident, Germain disclosed her true identity to Gauss. He replied,

How can I describe my astonishment and admiration on seeing my esteemed correspondent M leBlanc metamorphosed into this celebrated person. . . when a woman, because of her sex, our customs and prejudices, encounters infinitely more obstacles than men in familiarizing herself with [number theory's] knotty problems, yet overcomes these fetters and penetrates that which is most hidden, she doubtless has the most noble courage, extraordinary talent, and superior genius.

Gauss' letters to Olbers show that his praise for Germain was sincere. In the same 1807 letter, Sophie claimed that if xⁿ + yⁿ is of the form h² + nf², then x + y is also of that form. Gauss replied with a counterexample: 15¹¹ + 8¹¹ can be written as h² + 11f², but 15 + 8 cannot.

Although Gauss thought well of Germain, his replies to her letters were often delayed, and he generally did not review her work. Eventually his interests turned away from number theory, and in 1809 the letters ceased. Despite the friendship of Germain and Gauss, they never met.

When Germain's correspondence with Gauss ceased, she took interest in a contest sponsored by the Paris Academy of Sciences concerning Ernst Chladni's experiments with vibrating metal plates. The object of the competition, as stated by the Academy, was “to give the mathematical theory of the vibration of an elastic surface and to compare the theory to experimental evidence." Lagrange's comment that a solution to the problem would require the invention of a new branch of analysis deterred all but two contestants, Denis Poisson and Germain. Then Poisson was elected to the Academy, thus becoming a judge instead of a contestant, and leaving Germain as the only entrant to the competition.

In 1809 Germain began work. Legendre assisted by giving her equations, references, and current research. She submitted her paper early in the fall of 1811, and did not win the prize. The judging commission felt that “the true equations of the movement were not established,” even though “the experiments presented ingenious results.” Lagrange was able to use Germain's work to derive an equation that was “correct under special assumptions.”

The contest was extended by two years, and Germain decided to try again for the prize. At first Legendre continued to offer support, but then he refused all help. Germain's anonymous 1813 submission was still littered with mathematical errors, especially involving double integrals, and it received only an honorable mention because “the fundamental base of the theory [of elastic surfaces] was not established." The contest was extended once more, and Germain began work on her third attempt. This time she consulted with Poisson. In 1814 he published his own work on elasticity, and did not acknowledge Germain's help (although he had worked with her on the subject and, as a judge on the Academy commission, had had access to her work).

Germain submitted her third paper, “Recherches sur la théorie des surfaces élastique” under her own name, and on 8 January 1816 she became the first woman to win a prize from the Paris Academy of Sciences. She did not appear at the ceremony to receive her award. Although Germain had at last been awarded the prix extraordinaire, the Academy was still not fully satisfied. Sophie had derived the correct differential equation, but her method did not predict experimental results with great accuracy, as she had relied on an incorrect equation from Euler, which led to incorrect boundary conditions. Here is Germain's final equation:

where N² is a constant.

After winning the Academy contest, she was still not able to attend its sessions because of the Academy's tradition of excluding women other than the wives of members. Seven years later this tradition was broken when she made friends with Joseph Fourier, a secretary of the Academy, who obtained tickets to the sessions for her.

Germain published her prize winning essay at her own expense in 1821, mostly because she wanted to present her work in opposition to that of Poisson. In the essay she pointed out some of the errors in her method.

In 1826 she submitted a revised version of her 1821 essay to the Academy. According to Andrea del Centina, a math professor at the University of Ferrara in Italy, the revision included attempts to clarify her work by “introducing certain simplifying hypotheses." This put the Academy in an awkward position, as they felt the paper to be “inadequate and trivial,” but they did not want to “treat her as a professional colleague, as they would any man, by simply rejecting the work.” So Augustin - Louis Cauchy, who had been appointed to review her work, recommended she publish it, and she followed his advice.

One further work of Germain's on elasticity was published posthumously in 1831: her “Memoir sur la courbure des surfaces.” She used the mean curvature in her research.

Germain's best work was in number theory, and her most significant contribution to number theory dealt with Fermat's Last Theorem. In 1815, after the elasticity contest, the Academy offered a prize for a proof of Fermat's Last Theorem. It reawakened Germain's interest in number theory, and she wrote to Gauss again after ten years of no correspondence.

In the letter, Germain said that number theory was her preferred field, and that it was in her mind all the time she was studying elasticity. She outlined a strategy for a general proof of Fermat's Last Theorem, including a proof for a special case. Germain's letter to Gauss contained the first substantial progress toward a proof in 200 years. She asked Gauss if her approach to the theorem was worth pursuing. Gauss never answered.

Fermat's Last Theorem is commonly divided into two cases. Case 1 involves all p that do not divide any of x, y, or z. Case 2 includes all p that divide at least one of x, y, or z. Germain proposed the following, commonly called “Sophie Germain's Theorem”:

Let p be an odd prime. If there exists an auxiliary prime P = 2Np + 1 such that:

1. if x^p + y^p + z^p = 0 (mod P) then P divides xyz, and
2. p is not a p^th power residue (mod P).

Then the first case of Fermat's Last Theorem holds true for p.

Germain used this result to prove the first case of Fermat's Last Theorem for all odd primes p<100, but according to Andrea del Centina, “she had actually shown that it holds for every exponent p<197.” L.E. Dickson later used Germain's theorem to prove Fermat's Last Theorem for odd primes less than 1700.

In an unpublished manuscript entitled Remarque sur l’impossibilité de satisfaire en nombres entiers a l’équation x^p + y^p = z^p, Germain showed that any counterexamples to Fermat's theorem for p>5 must be numbers “whose size frightens the imagination,” around 40 digits long. Sophie did not publish this work. Her brilliant theorem is known only because of the footnote in Legendre's treatise on number theory, where he used it to prove Fermat's Last Theorem for p = 5. Germain also proved or nearly proved several results that were attributed to Lagrange or were rediscovered years later. Del Centina states that “after almost two hundred years her ideas were still central”, but ultimately her method did not work.

In addition to mathematics, Germain studied philosophy and psychology. She wanted to classify facts and generalize them into laws that could form a system of psychology and sociology, which were then just coming into existence. Her philosophy was highly praised by Auguste Comte.

Two of her philosophical works, Pensées diverses and Considérations générales sur l'état des sciences et des letteres aux différentes epoques de leur culture, were published, both posthumously. This was due in part to the efforts of Lherbette, her nephew, who collected her philosophical writings and published them. Pensées is a history of science and mathematics with Sophie's commentary. In Considérations, the work admired by Comte, Sophie argues that there are no differences between the sciences and the humanities.

In 1829 Germain learned she had breast cancer. Despite the pain, she continued to work. In 1831 Crelle's Journal published her paper on the curvature of elastic surfaces and “a note about finding y and z in 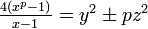." And American University's Gray records, “She also published in Annales de chimie et de physique an examination of principles which led to the discovery of the laws of equilibrium and movement of elastic solids." On June 27 of 1831, she died in the house at 13 rue de Savoie.

Despite Germain's intellectual achievements, her death certificate lists her as a “rentière – annuitant” (property holder), not a “mathematicienne." But her work was not unappreciated by everyone. When the matter of honorary degrees came up at the University of Göttingen six years after Germain's death, Gauss lamented, “[Germain] proved to the world that even a woman can accomplish something worthwhile in the most rigorous and abstract of the sciences and for that reason would well have deserved an honorary degree."

Germain's resting place in the Père Lachaise Cemetery in Paris is marked by a crumbling gravestone. At the centennial celebration of her life, a street and a girls' school were named after her, and a plaque was placed at the house where she died. The school houses a bust commissioned by the Paris City Council.

E. Dubouis defined a sophien of a prime n to be a prime θ where θ = kn + 1, for such n that yield θ such that xⁿ = yⁿ + 1 (mod θ) has no solutions when x and y are prime to n.

A Sophie Germain prime is a prime p such that 2p + 1 is also prime.

The Germain curvature (also called mean curvature) is 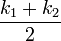, when k₁ and k₂ are the maximum and minimum values of the normal curvature.

Sophie Germain's Identity states that for any {x,y}, then,

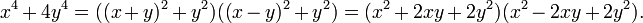
Vesna Petrovich, a graduate of the University of Michigan, found that the educated world's response to the publication in 1821 of Germain's prize winning essay “ranged from polite to indifferent". Yet, some critics had high praise for it. Of her essay in 1821, Cauchy said, “[it] was a work for which the name of its author and the importance of the subject both deserved the attention of mathematicians." H.J. Mozans, whose biography of Germain "is inaccurate and the notes and bibliography are unreliable", but is nevertheless interesting, quotes the mathematician Claude - Louis Navier as saying, "it is a work which few men are able to read and which only one woman was able to write."

Germain's contemporaries also had good things to say relating to her work in mathematics. Osen relates that “Baron de Prony called her the Hypatia of the nineteenth century,” and “J.J Biot wrote, in the Journal de Savants, that she had probably penetrated the science of mathematics more deeply than any other of her sex." Gauss certainly thought highly of her, and he recognized that European culture presented special difficulties to a woman in mathematics.

The modern view generally acknowledges that although Germain had great talent as a mathematician, her haphazard education had left her without the strong base she needed to truly excel. As explained by Gray, “Germain's work in elasticity suffered generally from an absence of rigor, which might be attributed to her lack of formal training in the rudiments of analysis." Petrovich adds, “This proved to be a major handicap when she could no longer be regarded as a young prodigy to be admired but was judged by her peer mathematicians.”

Notwithstanding the problems with Germain's theory of vibrations, Gray states that “Germain's work was fundamental in the development of a general theory of elasticity.” H.J. Mozans writes, however, that when the Eiffel tower was built and the architects inscribed the names of 72 scientists whose fundamental work in elasticity theory had made construction of the tower possible, Germain's name was not among them. “Was she excluded from this list... because she was a woman? It would seem so."

Concerning her early work in number theory, J.H. Sampson, author of “Sophie Germain and the Theory of Numbers,” states, “She was clever with formal algebraic manipulations; but there is little evidence that she really understood the Disquisitiones, and her work of that period that has come down to us seems to touch only on rather superficial matters." Gray adds that “The inclination of sympathetic mathematicians to praise her work rather than to provide substantive criticism from which she might learn was crippling to her mathematical development." Yet Marilyn Bailey Ogilvie, Curator of the History of Science Collections and Professor of the History of Science at the University of Oklahoma recognizes that “Sophie Germain's creativity manifested itself in pure and applied mathematics... [she] provided imaginative and provocative solutions to several important problems," and, as Petrovich proposes, it may have been her very lack of training that gave her her unique insights and approaches. Louis Bucciarelli and Nancy Dworsky, Germain's biographers, summarize as follows: “All the evidence argues that Sophie Germain had a mathematical brilliance that never reached fruition due to a lack of rigorous training available only to men."

Guy Terjanian is a French - Armenian mathematician who has worked on algebraic number theory. He achieved his Ph.D under Claude Chevalley in 1966, and at that time published a counterexample to the original form of a conjecture of Emil Artin, which suitably modified had just been proved as the Ax - Kochen theorem.

In 1977, he proved that if p is an odd prime number, and the natural numbers x, y and z satisfy x^2p + y^2p = z^2p, then 2p must divide x or y.

Born in California, Adleman grew up in San Francisco, and attended the University of California, Berkeley, where he received his BA degree in mathematics in 1968 and his Ph.D. degree in EECS in 1976. In 1994, his paper Molecular Computation of Solutions To Combinatorial Problems described the experimental use of DNA as a computational system. In it, he solved a seven - node instance of the Hamiltonian Graph problem, an NP-complete problem similar to the traveling salesman problem. While the solution to a seven - node instance is trivial, this paper is the first known instance of the successful use of DNA to compute an algorithm. DNA computing has been shown to have potential as a means to solve several other large scale combinatorial search problems.

In 2002, he and his research group managed to solve a 'nontrivial' problem using DNA computation. Specifically, they solved a 20 variable SAT problem having more than 1 million potential solutions. They did it in a manner similar to the one Adleman used in his seminal 1994 paper. First, a mixture of DNA strands logically representative of the problem's solution space was synthesized. This mixture was then operated upon algorithmically using biochemical techniques to winnow out the 'incorrect' strands, leaving behind only those strands that 'satisfied' the problem. Analysis of the nucleotide sequence of these remaining strands revealed 'correct' solutions to the original problem.

For his contribution to the invention of the RSA cryptosystem, Adleman, along with Ron Rivest and Adi Shamir, has been a recipient of the 1996 Paris Kanellakis Theory and Practice Award and the 2002 ACM Turing Award, often called the Nobel Prize of Computer Science.

Adleman was elected a Fellow of the American Academy of Arts and Sciences in 2006. He is one of the original discoverers of the Adleman - Pomerance - Rumely primality test. Fred Cohen, in his 1984 paper, Experiments with Computer Viruses has credited Adleman with coining the term "virus". He was also the mathematical consultant on the movie Sneakers. Adleman is also an amateur boxer and has sparred with James Toney. He is also widely referred to as the Father of DNA Computing. He is a member of the National Academy of Engineering and the National Academy of Sciences.

Currently, Adleman is working on the mathematical theory of Strata.

David Rodney "Roger" Heath - Brown F.R.S. (born 12 October 1952), is a British mathematician working in the field of analytic number theory. He was an undergraduate and graduate student of Trinity College, Cambridge; his research supervisor was Alan Baker. In 1979 he moved to the University of Oxford, where since 1999 he has held a professorship in pure mathematics.

Heath - Brown is known for many striking results. These include an approximate solution to Artin's conjecture on primitive roots, to the effect that out of 3, 5, 7 (or any three similar multiplicatively - independent square - free integers), one at least is a primitive root modulo p, for infinitely many prime numbers p. He also proved that there are infinitely many prime numbers of the form x³ + 2y³. In collaboration with S. J. Patterson in 1978 he proved the Kummer conjecture on cubic Gauss sums in its equidistribution form. He has applied Burgess's method on character sums to the ranks of elliptic curves in families. He proved that every non - singular cubic form over the rational numbers in at least ten variables represents 0. Heath - Brown also showed that Linnik's constant is less than or equal to 5.5.

The London Mathematical Society has awarded Heath - Brown the Junior Berwick Prize (1981), the Senior Berwick Prize (1996), and the Pólya Prize (2009). He was made a Fellow of the Royal Society in 1993, and a corresponding member of the Göttingen Academy of Sciences in 1999.

On 13 October 2010, in reference to the fact that a mother had given birth to three babies on the same date in different years, Heath Brown was quoted in the Daily Mail as stating that: "...the odds of the couple's children all being born on the same date were 48,627,125 to one." A number of readers appended comments to the article disagreeing with Heath - Brown's calculations.

Fouvry Etienne is a French mathematician, with the analytic theory of numbers employed.

Fouvry studied at the Ecole Normale Superieure in 1981 and at the University of Bordeaux under Henryk Iwaniec (and Jean - Marc Deshouillers) PhD (repartition of the suites dans les progressions arithmetique). He is a professor at the University of Paris - Sud in Orsay.

Fouvry applied methods of analytic number theory to the conjecture of Fermat. Based on his work, Roger Heath - Brown and Leonard Adleman proved in 1985 the first case of Fermat's conjecture for infinitely many primes. A number theoretical result of Fouvry published in Inventiones Mathematicae in 1985, formed an important component in the proof that prime is in P by Agrawal, Kayal and Saxena (2001).

Together with Iwaniec, he obtained deep results on primes in arithmetic progressions over the Bombieri - Vinogradov Theorem addition, with applications in the theory of Twin Primes.

In addition to analytic number theory Fouvry also studied algebraic and algorithmic number theory, for example, Cohen - Lenstra heuristics.