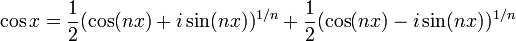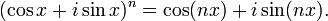Abraham de Moivre (26 May 1667 in Vitry - le - François, Champagne, France – 27 November 1754 in London, England) was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling. Among his fellow Huguenot exiles in England, he was a colleague of the editor and translator Pierre des Maizeaux.

De Moivre wrote a book on probability theory, The Doctrine of Chances, said to have been prized by gamblers. De Moivre first discovered Binet's formula, the closed form expression for Fibonacci numbers linking the nth power of φ to the nth Fibonacci number.

Abraham de Moivre was born in Vitry in Champagne on May 26, 1667. His father, Daniel de Moivre, was a surgeon who, though middle class, believed in the value of education. Though Abraham de Moivre's parents were Protestant, he first attended Christian Brothers' Catholic school in Vitry, which was unusually tolerant given religious tensions in France at the time. When he was eleven, his parents sent him to the Protestant Academy at Sedan, where he spent four years studying Greek under Jacques du Rondel. The Protestant Academy of Sedan had been founded in 1579 at the initiative of Françoise de Bourbon, widow of Henri - Robert de la Marck; in 1682 the Protestant Academy at Sedan was suppressed and de Moivre enrolled to study logic at Saumur for two years. Although mathematics was not part of his course work, de Moivre read several mathematical works on his own including Elements de mathematiques by Father Prestet and a short treatise on games of chance, De Ratiociniis in Ludo Aleae, by Christiaan Huygens. In 1684 he moved to Paris to study physics and for the first time had formal mathematics training with private lessons from Jacques Ozanam.

Religious persecution in France became severe when King Louis XIV issued the Edict of Fontainebleau in 1685, which revoked the Edict of Nantes, that had given substantial rights to French Protestants. It forbade Protestant worship and required that all children be baptized by Catholic priests. De Moivre was sent to the Prieure de Saint - Martin, a school the authorities sent Protestant children to for indoctrination into Catholicism. It is unclear when de Moivre left the Prieure de Saint - Martin and moved to England, as the records of the Prieure de Saint - Martin indicate that he left the school in 1688, but de Moivre and his brother presented themselves as Huguenots admitted to the Savoy Church in London on August 28, 1687.

By the time he arrived in London, de Moivre was a competent mathematician with a good knowledge of many of the standard texts. To make a living, de Moivre became a private tutor of mathematics, visiting his pupils or teaching in the coffee houses of London. De Moivre continued his studies of mathematics after visiting the Earl of Devonshire and seeing Newton’s recent book, Principia. Looking through the book, he realized it was far deeper than books he had studied previously, and was determined to read and understand it. However, as he was required to take extended walks around London to travel between his students, de Moivre had little time for study so he would tear pages from the book and carry them around in his pocket to read between lessons. Eventually de Moivre become so knowledgeable about the material that Newton referred questions to him, saying, “Go to Mr. de Moivre; he knows these things better than I do.”

By 1692, de Moivre became friends with Edmond Halley and soon after with Isaac Newton himself. In 1695, Halley communicated de Moivre’s first mathematics paper, which arose from his study of fluxions in the Principia, to the Royal Society. This paper was published in the Philosophical Transactions that same year. Shortly after publishing this paper de Moivre also generalized Newton’s famous Binomial Theorem into the Multinomial theorem. The Royal Society became apprised of this method in 1697 and made de Moivre a member two months later.

After de Moivre had been accepted, Halley encouraged him to turn his attention to astronomy. In 1705, de Moivre discovered, intuitively, that “the centripetal force of any planet is directly related to its distance from the center of the forces and reciprocally related to the product of the diameter of the evolute and the cube of the perpendicular on the tangent”. In other words, if a planet, M, follows an elliptical orbit around a focus F and has a point P where PM is tangent to the curve and FPM is a right angle so that FP is the perpendicular to the tangent, then the centripetal force at point P is proportional to F*M/(R*(F*P)³) where R is the radius of the curvature at M. Johann Bernoulli proved this formula in 1710.

Despite these successes, de Moivre was unable to obtain an appointment to a Chair of Mathematics at a university, which would have released him from his dependence on time consuming tutoring that burdened him more than it did most other mathematicians of the time. At least a part of the reason was a bias against his French origins.

In November 1697 he was elected a Fellow of the Royal Society and in 1712 was appointed to a commission set up by the society, alongside MM. Arbuthnot, Hill, Halley, Jones, Machin, Burnet, Robarts, Bonet, Aston and Taylor to review the claims of Newton and Leibniz as to who discovered calculus.

Throughout his life de Moivre remained poor. It is reported that he was a regular customer of Slaughter's Coffee House, St. Martin's Lane at Cranbourn Street, where he earned a little money from playing chess.

De Moivre continued studying the fields of probability and mathematics until his death in 1754 and several additional papers were published after his death. As he grew older, he became increasingly lethargic and needed longer sleeping hours. He noted that he was sleeping an extra 15 minutes each night and correctly calculated the date of his death on the day when the additional sleep time accumulated to 24 hours, November 27, 1754. He died in London and was buried at St Martin - in - the - Fields, although his body was later moved.

De Moivre pioneered the development of analytic geometry and the theory of probability by expanding upon the work of his predecessors, particularly Christiaan Huygens and several members of the Bernoulli family. He also produced the second textbook on probability theory, The Doctrine of Chances: a method of calculating the probabilities of events in play. (The first book about games of chance, Liber de ludo aleae ("On Casting the Die") , was written by Girolamo Cardano in the 1560s, but not published until 1663.) This book came out in four editions, 1711 in Latin, and 1718, 1738 and 1756 in English. In the later editions of his book, de Moivre gives the first statement of the formula for the normal distribution curve, the first method of finding the probability of the occurrence of an error of a given size when that error is expressed in terms of the variability of the distribution as a unit, and the first identification of the probable error calculation. Additionally, he applied these theories to gambling problems and actuarial tables.

An expression commonly found in probability is n! but before the days of calculators calculating n! for a large n was time consuming. In 1733 de Moivre proposed the formula for estimating a factorial as n! = cn^n+1/2e⁻ⁿ. He obtained an expression for the constant c but it was James Stirling who found that c was √(2π). Therefore, Stirling's approximation is as much due to de Moivre as it is to Stirling.

De Moivre also published an article called Annuities upon Lives, in which he revealed the normal distribution of the mortality rate over a person’s age. From this he produced a simple formula for approximating the revenue produced by annual payments based on a person’s age. This is similar to the types of formulas used by insurance companies today.

In 1707 de Moivre derived:

which he was able to prove for all positive integral values of n. In 1722 he suggested it in the more well known form of de Moivre's Formula:

In 1749 Euler proved this formula for any real n using Euler's formula, which makes the proof quite straightforward. This formula is important because it relates complex numbers and trigonometry. Additionally, this formula allows the derivation of useful expressions for cos(nx) and sin(nx) in terms of cos(x) and sin(x).