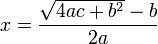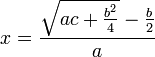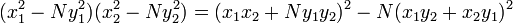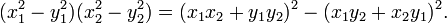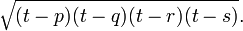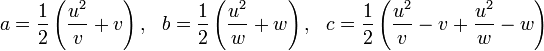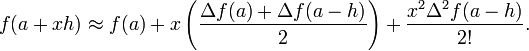Brahmagupta is considered to be the most indispensable mathematician in history of mathematics. He is immortalized as the discoverer of zero. Brahmagupta is believed to have been born in 598 AD in Bhinmal city in the state of Rajasthan of Northwest India. In ancient times Bhillamala was the seat of power of the Gurjars. His father was Jisnugupta. He likely lived most of his life in Bhillamala (modern Bhinmal in Rajasthan) during the reign (and possibly under the patronage) of King Vyaghramukha. As a result, Brahmagupta is often referred to as Bhillamalacarya, that is, the teacher from Bhillamala. He was the head of the astronomical observatory at Ujjain, and during his tenure there wrote four texts on mathematics and astronomy: the Cadamekela in 624, the Brahmasphutasiddhanta in 628, the Khandakhadyaka in 665, and the Durkeamynarda in 672. The Brahmasphutasiddhanta (Corrected Treatise of Brahma) is arguably his most famous work. The historian al-Biruni (c. 1050) in his book Tariq al-Hind states that the Abbasid caliph al-Ma'mun had an embassy in India and from India a book was brought to Baghdad which was translated into Arabic as Sindhind. It is generally presumed that Sindhind is none other than Brahmagupta's Brahmasphuta - siddhanta.

Although Brahmagupta was familiar with the works of astronomers following the tradition of Aryabhatiya, it is not known if he was familiar with the work of Bhaskara I, a contemporary. Brahmagupta had a plethora of criticism directed towards the work of rival astronomers, and in his Brahmasphuta - siddhanta is found one of the earliest attested schisms among Indian mathematicians. The division was primarily about the application of mathematics to the physical world, rather than about the mathematics itself. In Brahmagupta's case, the disagreements stemmed largely from the choice of astronomical parameters and theories. Critiques of rival theories appear throughout the first ten astronomical chapters and the eleventh chapter is entirely devoted to criticism of these theories, although no criticisms appear in the twelfth and eighteenth chapters.

Brahmagupta was the first to use zero as a number. He gave rules to compute with zero. Brahmagupta used negative numbers and zero for computing. The modern rule that two negative numbers multiplied together equals a positive number first appears in Brahmasputa siddhanta. Brahmagupta's most famous work is his Brahmasphuta siddhanta. It is composed in elliptic verse, as was common practice in Indian mathematics, and consequently has a poetic ring to it. As no proofs are given, it is not known how Brahmagupta's mathematics was derived.

Brahmagupta gave the solution of the general linear equation in chapter eighteen of Brahmasphuta siddhanta,

The difference between rupas, when inverted and divided by the difference of the unknowns, is the unknown in the equation. The rupas are [subtracted on the side] below that from which the square and the unknown are to be subtracted.

Which is a solution equivalent to 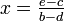, where rupas represents constants. He further gave two equivalent solutions to the general quadratic equation,

18.44. Diminish by the middle [number] the square - root of the rupas multiplied by four times the square and increased by the square of the middle [number]; divide the remainder by twice the square. [The result is] the middle [number].
18.45. Whatever is the square - root of the rupas multiplied by the square [and] increased by the square of half the unknown, diminish that by half the unknown [and] divide [the remainder] by its square. [The result is] the unknown.

Which are, respectively, solutions equivalent to,

and

He went on to solve systems of simultaneous indeterminate equations stating that the desired variable must first be isolated, and then the equation must be divided by the desired variable's coefficient. In particular, he recommended using "the pulverizer" to solve equations with multiple unknowns.

18.51. Subtract the colors different from the first color. [The remainder] divided by the first [color's coefficient] is the measure of the first. [Terms] two by two [are] considered [when reduced to] similar divisors, [and so on] repeatedly. If there are many [colors], the pulverizer [is to be used].

Like the algebra of Diophantus, the algebra of Brahmagupta was syncopated. Addition was indicated by placing the numbers side by side, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, similar to our notation but without the bar. Multiplication, evolution, and unknown quantities were represented by abbreviations of appropriate terms. The extent of Greek influence on this syncopation, if any, is not known and it is possible that both Greek and Indian syncopation may be derived from a common Babylonian source.

Four fundamental operations (addition, subtraction, multiplication and division) were known to many cultures before Brahmagupta. This current system is based on the Hindu Arabic number system and first appeared in Brahmasputa siddhanta. Brahmagupta describes the multiplication as thus “The multiplicand is repeated like a string for cattle, as often as there are integrant portions in the multiplier and is repeatedly multiplied by them and the products are added together. It is multiplication. Or the multiplicand is repeated as many times as there are component parts in the multiplier”. But the sumerian methods were cumbersome and diffiicult as the Greek method and we don't use today. Indian arithmetic was known in Medieval Europe as "Modus Indoram" meaning method of the Indians. In Brahmasputha Siddhanta, Multiplication was named Gomutrika. In the beginning of chapter twelve of his Brahmasphuta siddhanta, entitled Calculation, Brahmagupta details operations on fractions. The reader is expected to know the basic arithmetic operations as far as taking the square root, although he explains how to find the cube and cube - root of an integer and later gives rules facilitating the computation of squares and square roots. He then gives rules for dealing with five types of combinations of fractions, 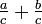, , 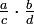, , 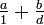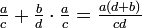and .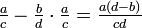

Brahmagupta then goes on to give the sum of the squares and cubes of the first n integers.

12.20. The sum of the squares is that [sum] multiplied by twice the [number of] step[s] increased by one [and] divided by three. The sum of the cubes is the square of that [sum] Piles of these with identical balls [can also be computed].

It is important to note here Brahmagupta found the result in terms of the sum of the first n integers, rather than in terms of n as is the modern practice.

He gives the sum of the squares of the first n natural numbers as n(n+1)(2n+1)/6 and the sum of the cubes of the first n natural numbers as (n(n+1)/2)².

Brahmagupta's Brahmasphuṭa siddhanta is the very first book that mentions zero as a number, hence Brahmagupta is considered as the man who found zero. He gave rules of using zero with negative and positive numbers. Zero plus a positive number is the positive number and negative number plus zero is a negative number etc. The Brahmasphuta siddhanta is the earliest known text to treat zero as a number in its own right, rather than as simply a placeholder digit in representing another number as was done by the Babylonians or as a symbol for a lack of quantity as was done by Ptolemy and the Romans. In chapter eighteen of his Brahmasphuta siddhanta, Brahmagupta describes operations on negative numbers. He first describes addition and subtraction,

18.30. [The sum] of two positives is positives, of two negatives negative; of a positive and a negative [the sum] is their difference; if they are equal it is zero. The sum of a negative and zero is negative, [that] of a positive and zero positive, [and that] of two zeros zero.
[...]
18.32. A negative minus zero is negative, a positive [minus zero] positive; zero [minus zero] is zero. When a positive is to be subtracted from a negative or a negative from a positive, then it is to be added.

He goes on to describe multiplication,

18.33. The product of a negative and a positive is negative, of two negatives positive, and of positives positive; the product of zero and a negative, of zero and a positive, or of two zeros is zero.

But his description of division by zero differs from our modern understanding,

18.34. A positive divided by a positive or a negative divided by a negative is positive; a zero divided by a zero is zero; a positive divided by a negative is negative; a negative divided by a positive is [also] negative.
18.35. A negative or a positive divided by zero has that [zero] as its divisor, or zero divided by a negative or a positive [has that negative or positive as its divisor]. The square of a negative or of a positive is positive; [the square] of zero is zero. That of which [the square] is the square is [its] square - root.

Here Brahmagupta states that 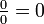 and as for the question of  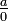where 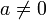 he did not commit himself. His rules for arithmetic on negative numbers and zero are quite close to the modern understanding, except that in modern mathematics division by zero is left undefined.

In chapter twelve of his Brahmasphuta siddhanta, Brahmagupta finds Pythagorean triples,

12.39. The height of a mountain multiplied by a given multiplier is the distance to a city; it is not erased. When it is divided by the multiplier increased by two it is the leap of one of the two who make the same journey.

or in other words, for a given length m and an arbitrary multiplier x, let a = mx and b = m + mx/(x + 2). Then m, a, and b form a Pythagorean triple.

Brahmagupta went on to give a recurrence relation for generating solutions to certain instances of Diophantine equations of the second degree such as Nx² + 1 = y² (called Pell's equation) by using the Euclidean algorithm. The Euclidean algorithm was known to him as the "pulverizer" since it breaks numbers down into ever smaller pieces.

The nature of squares:
18.64. [Put down] twice the square-root of a given square by a multiplier and increased or diminished by an arbitrary [number]. The product of the first [pair], multiplied by the multiplier, with the product of the last [pair], is the last computed.
18.65. The sum of the thunderbolt products is the first. The additive is equal to the product of the additives. The two square - roots, divided by the additive or the subtractive, are the additive rupas.

The key to his solution was the identity,

which is a generalization of an identity that was discovered by Diophantus,

Using his identity and the fact that if (x₁, y₁) and (x₂, y₂) are solutions to the equations x² − Ny² = k₁ and x² − Ny² = k₂, respectively, then (x₁x₂ + Ny₁y₂, x₁y₂ + x₂y₁) is a solution to x² − Ny² = k₁k₂, he was able to find integral solutions to Pell's equation through a series of equations of the form x² − Ny² = k_i. Unfortunately, Brahmagupta was not able to apply his solution uniformly for all possible values of N, rather he was only able to show that if x² − Ny² = k has an integral solution for k = ±1, ±2, or ±4, then x² − Ny² = 1 has a solution. The solution of the general Pell's equation would have to wait for Bhaskara II in c. 1150 CE.

Brahmagupta's most famous result in geometry is his formula for cyclic quadrilaterals. Given the lengths of the sides of any cyclic quadrilateral, Brahmagupta gave an approximate and an exact formula for the figure's area,

12.21. The approximate area is the product of the halves of the sums of the sides and opposite sides of a triangle and a quadrilateral. The accurate [area] is the square root from the product of the halves of the sums of the sides diminished by [each] side of the quadrilateral.

So given the lengths p, q, r and s of a cyclic quadrilateral, the approximate area is 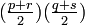 while, letting 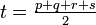, the exact area is

Although Brahmagupta does not explicitly state that these quadrilaterals are cyclic, it is apparent from his rules that this is the case. Heron's formula is a special case of this formula and it can be derived by setting one of the sides equal to zero.

Brahmagupta dedicated a substantial portion of his work to geometry. One theorem states that the two lengths of a triangle's base when divided by its altitude then follows,

12.22. The base decreased and increased by the difference between the squares of the sides divided by the base; when divided by two they are the true segments. The perpendicular [altitude] is the square - root from the square of a side diminished by the square of its segment.

Thus the lengths of the two segments are .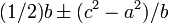

He further gives a theorem on rational triangles. A triangle with rational sides a, b, c and rational area is of the form:

for some rational numbers u, v, and w.

Brahmagupta continues,

12.23. The square - root of the sum of the two products of the sides and opposite sides of a non - unequal quadrilateral is the diagonal. The square of the diagonal is diminished by the square of half the sum of the base and the top; the square - root is the perpendicular [altitudes].

So, in a "non - unequal" cyclic quadrilateral (that is, an isosceles trapezoid), the length of each diagonal is .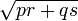

He continues to give formulas for the lengths and areas of geometric figures, such as the circumradius of an isosceles trapezoid and a scalene quadrilateral, and the lengths of diagonals in a scalene cyclic quadrilateral. This leads up to Brahmagupta's famous theorem,

12.30-31. Imaging two triangles within [a cyclic quadrilateral] with unequal sides, the two diagonals are the two bases. Their two segments are separately the upper and lower segments [formed] at the intersection of the diagonals. The two [lower segments] of the two diagonals are two sides in a triangle; the base [of the quadrilateral is the base of the triangle]. Its perpendicular is the lower portion of the [central] perpendicular; the upper portion of the [central] perpendicular is half of the sum of the [sides] perpendiculars diminished by the lower [portion of the central perpendicular].

In verse 40, he gives values of π,

12.40. The diameter and the square of the radius [each] multiplied by 3 are [respectively] the practical circumference and the area [of a circle]. The accurate [values] are the square - roots from the squares of those two multiplied by ten.

So Brahmagupta uses 3 as a "practical" value of π, and 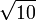 as an "accurate" value of π.

In some of the verses before verse 40, Brahmagupta gives constructions of various figures with arbitrary sides. He essentially manipulated right triangles to produce isosceles triangles, scalene triangles, rectangles, isosceles trapezoids, isosceles trapezoids with three equal sides, and a scalene cyclic quadrilateral.

After giving the value of pi, he deals with the geometry of plane figures and solids, such as finding volumes and surface areas (or empty spaces dug out of solids). He finds the volume of rectangular prisms, pyramids, and the frustum of a square pyramid. He further finds the average depth of a series of pits. For the volume of a frustum of a pyramid, he gives the "pragmatic" value as the depth times the square of the mean of the edges of the top and bottom faces, and he gives the "superficial" volume as the depth times their mean area.

In Chapter 2 of his Brahmasphuta siddhanta, entitled Planetary True Longitudes, Brahmagupta presents a sine table:

2.2-5. The sines: The Progenitors, twins; Ursa Major, twins, the Vedas; the gods, fires, six; flavors, dice, the gods; the moon, five, the sky, the moon; the moon, arrows, suns [...]

Here Brahmagupta uses names of objects to represent the digits of place - value numerals, as was common with numerical data in Sanskrit treatises. Progenitors represents the 14 Progenitors ("Manu") in Indian cosmology or 14, "twins" means 2, "Ursa Major" represents the seven stars of Ursa Major or 7, "Vedas" refers to the 4 Vedas or 4, dice represents the number of sides of the tradition die or 6, and so on. This information can be translated into the list of sines, 214, 427, 638, 846, 1051, 1251, 1446, 1635, 1817, 1991, 2156, 2312, 1459, 2594, 2719, 2832, 2933, 3021, 3096, 3159, 3207, 3242, 3263, and 3270, with the radius being 3270.

In 665 Brahmagupta devised and used a special case of the Newton – Stirling interpolation formula of the second order to interpolate new values of the sine function from other values already tabulated. The formula gives an estimate for the value of a function f at a value a + xh of its argument (with h > 0 and −1 ≤ x ≤ 1) when its value is already known at a − h,  a and a + h.

The formula for the estimate is:

where Δ is the first-order forward-difference operator, i.e.

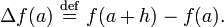
It was through the Brahmasphuta siddhanta that the Arabs learned of Indian astronomy. Edward Saxhau stated that "Brahmagupta, it was he who taught Arabs astronomy". The famous Abbasid caliph Al-Mansur (712 – 775) founded Baghdad, which is situated on the banks of the Tigris, and made it a center of learning. The caliph invited a scholar of Ujjain by the name of Kankah in 770 A.D. Kankah used the Brahmasphuta siddhanta to explain the Hindu system of arithmetic astronomy. Muhammad al-Fazari translated Brahmugupta's work into Arabic upon the request of the caliph.

In chapter seven of his Brahmasphuta siddhanta, entitled Lunar Crescent, Brahmagupta rebuts the idea that the Moon is farther from the Earth than the Sun, an idea which is maintained in scriptures. He does this by explaining the illumination of the Moon by the Sun.

7.1. If the moon were above the sun, how would the power of waxing and waning, etc., be produced from calculation of the [longitude of the] moon? the near half [would be] always bright.
7.2. In the same way that the half seen by the sun of a pot standing in sunlight is bright, and the unseen half dark, so is [the illumination] of the moon [if it is] beneath the sun.
7.3. The brightness is increased in the direction of the sun. At the end of a bright [i.e. waxing] half - month, the near half is bright and the far half dark. Hence, the elevation of the horns [of the crescent can be derived] from calculation. [...]

He explains that since the Moon is closer to the Earth than the Sun, the degree of the illuminated part of the Moon depends on the relative positions of the Sun and the Moon, and this can be computed from the size of the angle between the two bodies.

Some of the important contributions made by Brahmagupta in astronomy are: methods for calculating the position of heavenly bodies over time (ephemerides), their rising and setting, conjunctions, and the calculation of solar and lunar eclipses. Brahmagupta criticized the Puranic view that the Earth was flat or hollow. Instead, he observed that the Earth and heaven were spherical and that the Earth is moving. In 1030, the Muslim astronomer Abu al-Rayhan al-Biruni, in his Ta'rikh al-Hind, later translated into Latin as Indica, commented on Brahmagupta's work and wrote that critics argued:

"If such were the case, stones would and trees would fall from the earth."

According to al-Biruni, Brahmagupta responded to these criticisms with the following argument on gravitation:

"On the contrary, if that were the case, the earth would not vie in keeping an even and uniform pace with the minutes of heaven, the pranas of the times. [...] All heavy things are attracted towards the center of the earth. [...] The earth on all its sides is the same; all people on earth stand upright, and all heavy things fall down to the earth by a law of nature, for it is the nature of the earth to attract and to keep things, as it is the nature of water to flow, that of fire to burn, and that of wind to set in motion… The earth is the only low thing, and seeds always return to it, in whatever direction you may throw them away, and never rise upwards from the earth."

About the Earth's gravity he said: "Bodies fall towards the earth as it is in the nature of the earth to attract bodies, just as it is in the nature of water to flow."