Johannes Kepler (December 27, 1571 – November 15, 1630) was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican Astronomy. These works also provided one of the foundations for Isaac Newton's theory of universal gravitation.

During his career, Kepler was a mathematics teacher at a seminary school in Graz, Austria, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to astronomer Tycho Brahe, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He was also a mathematics teacher in Linz, Austria, and an adviser to General Wallenstein. Additionally, he did fundamental work in the field of optics, invented an improved version of the refracting telescope (the Keplerian Telescope), and mentioned the telescopic discoveries of his contemporary Galileo Galilei.

Kepler lived in an era when there was no clear distinction between astronomy and astrology, but there was a strong division between astronomy (a branch of mathematics within the liberal arts) and physics (a branch of natural philosophy). Kepler also incorporated religious arguments and reasoning into his work, motivated by the religious conviction and belief that God had created the world according to an intelligible plan that is accessible through the natural light of reason. Kepler described his new astronomy as "celestial physics", as "an excursion into Aristotle's Metaphysics", and as "a supplement to Aristotle's On the Heavens", transforming the ancient tradition of physical cosmology by treating astronomy as part of a universal mathematical physics.

Johannes Kepler was born on December 27, 1571, at the Free Imperial City of Weil der Stadt (now part of the Stuttgart Region in the German state of Baden - Württemberg, 30 km west of Stuttgart's center). His grandfather, Sebald Kepler, had been Lord Mayor of that town but, by the time Johannes was born, he had two brothers and one sister and the Kepler family fortune was in decline. His father, Heinrich Kepler, earned a precarious living as a mercenary, and he left the family when Johannes was five years old. He was believed to have died in the Eighty Years' War in the Netherlands. His mother Katharina Guldenmann, an inn keeper's daughter, was a healer and herbalist who was later tried for witchcraft. Born prematurely, Johannes claimed to have been weak and sickly as a child. Nevertheless, he often impressed travelers at his grandfather's inn with his phenomenal mathematical faculty.

He was introduced to astronomy at an early age, and developed a love for it that would span his entire life. At age six, he observed the Great Comet of 1577, writing that he "was taken by [his] mother to a high place to look at it." At age nine, he observed another astronomical event, a lunar eclipse in 1580, recording that he remembered being "called outdoors" to see it and that the moon "appeared quite red". However, childhood smallpox left him with weak vision and crippled hands, limiting his ability in the observational aspects of astronomy.

In 1589, after moving through grammar school, Latin school, and seminary at Maulbronn, Kepler attended Tübinger Stift at the University of Tübingen. There, he studied philosophy under Vitus Müller and theology under Jacob Heerbrand (a student of Philipp Melanchthon at Wittenberg), who also taught Michael Maestlin while he was a student, until he became Chancellor at Tübingen in 1590. He proved himself to be a superb mathematician and earned a reputation as a skillful astrologer, casting horoscopes for fellow students. Under the instruction of Michael Maestlin, Tübingen's professor of mathematics from 1583 to 1631, he learned both the Ptolemaic system and the Copernican system of planetary motion. He became a Copernican at that time. In a student disputation, he defended heliocentrism from both a theoretical and theological perspective, maintaining that the Sun was the principal source of motive power in the universe. Despite his desire to become a minister, near the end of his studies Kepler was recommended for a position as teacher of mathematics and astronomy at the Protestant school in Graz (later the University of Graz). He accepted the position in April 1594, at the age of 23.

Johannes Kepler's first major astronomical work, Mysterium Cosmographicum (The Cosmographic Mystery), was the first published defense of the Copernican system. Kepler claimed to have had an epiphany on July 19, 1595, while teaching in Graz, demonstrating the periodic conjunction of Saturn and Jupiter in the zodiac; he realized that regular polygons bound one inscribed and one circumscribed circle at definite ratios, which, he reasoned, might be the geometrical basis of the universe. After failing to find a unique arrangement of polygons that fit known astronomical observations (even with extra planets added to the system), Kepler began experimenting with 3 dimensional polyhedra. He found that each of the five Platonic solids could be uniquely inscribed and circumscribed by spherical orbs; nesting these solids, each encased in a sphere, within one another would produce six layers, corresponding to the six known planets — Mercury, Venus, Earth, Mars, Jupiter, and Saturn. By ordering the solids correctly — octahedron, icosahedron, dodecahedron, tetrahedron, cube — Kepler found that the spheres could be placed at intervals corresponding (within the accuracy limits of available astronomical observations) to the relative sizes of each planet’s path, assuming the planets circle the Sun. Kepler also found a formula relating the size of each planet’s orb to the length of its orbital period: from inner to outer planets, the ratio of increase in orbital period is twice the difference in orb radius. However, Kepler later rejected this formula, because it was not precise enough.

As he indicated in the title, Kepler thought he had revealed God’s geometrical plan for the universe. Much of Kepler’s enthusiasm for the Copernican system stemmed from his theological convictions about the connection between the physical and the spiritual; the universe itself was an image of God, with the Sun corresponding to the Father, the stellar sphere to the Son, and the intervening space between to the Holy Spirit. His first manuscript of Mysterium contained an extensive chapter reconciling heliocentrism with biblical passages that seemed to support geocentrism.

With the support of his mentor Michael Maestlin, Kepler received permission from the Tübingen university senate to publish his manuscript, pending removal of the Bible exegesis and the addition of a simpler, more understandable description of the Copernican system as well as Kepler’s new ideas. Mysterium was published late in 1596, and Kepler received his copies and began sending them to prominent astronomers and patrons early in 1597; it was not widely read, but it established Kepler’s reputation as a highly skilled astronomer. The effusive dedication, to powerful patrons as well as to the men who controlled his position in Graz, also provided a crucial doorway into the patronage system.

Though the details would be modified in light of his later work, Kepler never relinquished the Platonist polyhedral - spherist cosmology of Mysterium Cosmographicum. His subsequent main astronomical works were in some sense only further developments of it, concerned with finding more precise inner and outer dimensions for the spheres by calculating the eccentricities of the planetary orbits within it. In 1621 Kepler published an expanded second edition of Mysterium, half as long again as the first, detailing in footnotes the corrections and improvements he had achieved in the 25 years since its first publication.

In terms of the impact of Mysterium, it can be seen as an important first step in modernizing Copernicus' theory. There is no doubt that Copernicus' "De Revolutionibus" seeks to advance a sun centered system, but in this book he had to resort to Ptolemaic devices (viz., epicycles and eccentric circles) in order to explain the change in planets' orbital speed. Furthermore, Copernicus continued to use as a point of reference the center of the earth's orbit rather than that of the sun, as he says, "as an aid to calculation and in order not to confuse the reader by diverging too much from Ptolemy." Therefore, although the thesis of the "Mysterium Cosmographicum" was in error, modern astronomy owes much to this work "since it represents the first step in cleansing the Copernican system of the remnants of the Ptolemaic theory still clinging to it."

In December 1595, Kepler was introduced to Barbara Müller, a 23 year old widow (twice over) with a young daughter, Gemma van Dvijneveldt, and he began courting her. Müller, heiress to the estates of her late husbands, was also the daughter of a successful mill owner. Her father Jobst initially opposed a marriage despite Kepler's nobility; though he had inherited his grandfather's nobility, Kepler's poverty made him an unacceptable match. Jobst relented after Kepler completed work on Mysterium, but the engagement nearly fell apart while Kepler was away tending to the details of publication. However, church officials — who had helped set up the match — pressured the Müllers to honor their agreement. Barbara and Johannes were married on April 27, 1597.

In the first years of their marriage, the Keplers had two children (Heinrich and Susanna), both of whom died in infancy. In 1602, they had a daughter (Susanna); in 1604, a son (Friedrich); and in 1607, another son (Ludwig).

Following the publication of Mysterium and with the blessing of the Graz school inspectors, Kepler began an ambitious program to extend and elaborate his work. He planned four additional books: one on the stationary aspects of the universe (the Sun and the fixed stars); one on the planets and their motions; one on the physical nature of planets and the formation of geographical features (focused especially on Earth); and one on the effects of the heavens on the Earth, to include atmospheric optics, meteorology and astrology.

He also sought the opinions of many of the astronomers to whom he had sent Mysterium, among them Reimarus Ursus (Nicolaus Reimers Bär) — the imperial mathematician to Rudolph II and a bitter rival of Tycho Brahe. Ursus did not reply directly, but republished Kepler's flattering letter to pursue his priority dispute over (what is now called) the Tychonic system with Tycho. Despite this black mark, Tycho also began corresponding with Kepler, starting with a harsh but legitimate critique of Kepler's system; among a host of objections, Tycho took issue with the use of inaccurate numerical data taken from Copernicus. Through their letters, Tycho and Kepler discussed a broad range of astronomical problems, dwelling on lunar phenomena and Copernican theory (particularly its theological viability). But without the significantly more accurate data of Tycho's observatory, Kepler had no way to address many of these issues.

Instead, he turned his attention to chronology and "harmony," the numerological relationships among music, mathematics and the physical world, and their astrological consequences. By assuming the Earth to possess a soul (a property he would later invoke to explain how the sun causes the motion of planets), he established a speculative system connecting astrological aspects and astronomical distances to weather and other earthly phenomena. By 1599, however, he again felt his work limited by the inaccuracy of available data — just as growing religious tension was also threatening his continued employment in Graz. In December of that year, Tycho invited Kepler to visit him in Prague; on January 1, 1600 (before he even received the invitation), Kepler set off in the hopes that Tycho's patronage could solve his philosophical problems as well as his social and financial ones.

On February 4, 1600, Kepler met Tycho Brahe and his assistants Franz Tengnagel and Longomontanus at Benátky nad Jizerou (35 km from Prague), the site where Tycho's new observatory was being constructed. Over the next two months he stayed as a guest, analyzing some of Tycho's observations of Mars; Tycho guarded his data closely, but was impressed by Kepler's theoretical ideas and soon allowed him more access. Kepler planned to test his theory from Mysterium Cosmographicum based on the Mars data, but he estimated that the work would take up to two years (since he was not allowed to simply copy the data for his own use). With the help of Johannes Jessenius, Kepler attempted to negotiate a more formal employment arrangement with Tycho, but negotiations broke down in an angry argument and Kepler left for Prague on April 6. Kepler and Tycho soon reconciled and eventually reached an agreement on salary and living arrangements, and in June, Kepler returned home to Graz to collect his family.

Political and religious difficulties in Graz dashed his hopes of returning immediately to Tycho; in hopes of continuing his astronomical studies, Kepler sought an appointment as mathematician to Archduke Ferdinand. To that end, Kepler composed an essay — dedicated to Ferdinand — in which he proposed a force - based theory of lunar motion: "In Terra inest virtus, quae Lunam ciet" ("There is a force in the earth which causes the moon to move"). Though the essay did not earn him a place in Ferdinand's court, it did detail a new method for measuring lunar eclipses, which he applied during the July 10 eclipse in Graz. These observations formed the basis of his explorations of the laws of optics that would culminate in Astronomiae Pars Optica.

On August 2, 1600, after refusing to convert to Catholicism, Kepler and his family were banished from Graz. Several months later, Kepler returned, now with the rest of his household, to Prague. Through most of 1601, he was supported directly by Tycho, who assigned him to analyzing planetary observations and writing a tract against Tycho's (by then deceased) rival, Ursus. In September, Tycho secured him a commission as a collaborator on the new project he had proposed to the emperor: the Rudolphine Tables that should replace the Prutenic Tables of Erasmus Reinhold. Two days after Tycho's unexpected death on October 24, 1601, Kepler was appointed his successor as imperial mathematician with the responsibility to complete his unfinished work. The next 11 years as imperial mathematician would be the most productive of his life.

Kepler's primary obligation as imperial mathematician was to provide astrological advice to the emperor. Though Kepler took a dim view of the attempts of contemporary astrologers to precisely predict the future or divine specific events, he had been casting well received detailed horoscopes for friends, family and patrons since his time as a student in Tübingen. In addition to horoscopes for allies and foreign leaders, the emperor sought Kepler's advice in times of political trouble (though Kepler's recommendations were based more on common sense than the stars). Rudolph was actively interested in the work of many of his court scholars (including numerous alchemists) and kept up with Kepler's work in physical astronomy as well.

Officially, the only acceptable religious doctrines in Prague were Catholic and Utraquist, but Kepler's position in the imperial court allowed him to practice his Lutheran faith unhindered. The emperor nominally provided an ample income for his family, but the difficulties of the over - extended imperial treasury meant that actually getting hold of enough money to meet financial obligations was a continual struggle. Partly because of financial troubles, his life at home with Barbara was unpleasant, marred with bickering and bouts of sickness. Court life, however, brought Kepler into contact with other prominent scholars (Johannes Matthäus Wackher von Wackhenfels, Jost Bürgi, David Fabricius, Martin Bachazek, and Johannes Brengger, among others) and astronomical work proceeded rapidly.

As he slowly continued analyzing Tycho's Mars observations — now available to him in their entirety — and began the slow process of tabulating the Rudolphine Tables, Kepler also picked up the investigation of the laws of optics from his lunar essay of 1600. Both lunar and solar eclipses presented unexplained phenomena, such as unexpected shadow sizes, the red color of a total lunar eclipse, and the reportedly unusual light surrounding a total solar eclipse. Related issues of atmospheric refraction applied to all astronomical observations. Through most of 1603, Kepler paused his other work to focus on optical theory; the resulting manuscript, presented to the emperor on January 1, 1604, was published as Astronomiae Pars Optica (The Optical Part of Astronomy). In it, Kepler described the inverse - square law governing the intensity of light, reflection by flat and curved mirrors, and principles of pinhole cameras, as well as the astronomical implications of optics such as parallax and the apparent sizes of heavenly bodies. He also extended his study of optics to the human eye, and is generally considered by neuroscientists to be the first to recognize that images are projected inverted and reversed by the eye's lens onto the retina. The solution to this dilemma was not of particular importance to Kepler as he did not see it as pertaining to optics, although he did suggest that the image was later corrected "in the hollows of the brain" due to the "activity of the Soul." Today, Astronomiae Pars Optica is generally recognized as the foundation of modern optics (though the law of refraction is conspicuously absent).

In October 1604, a bright new evening star (SN 1604) appeared, but Kepler did not believe the rumors until he saw it himself. Kepler began systematically observing the star. Astrologically, the end of 1603 marked the beginning of a fiery trigon, the start of the ca. 800 year cycle of great conjunctions; astrologers associated the two previous such periods with the rise of Charlemagne (ca. 800 years earlier) and the birth of Christ (ca. 1600 years earlier), and thus expected events of great portent, especially regarding the emperor. It was in this context, as the imperial mathematician and astrologer to the emperor, that Kepler described the new star two years later in his De Stella Nova. In it, Kepler addressed the star's astronomical properties while taking a skeptical approach to the many astrological interpretations then circulating. He noted its fading luminosity, speculated about its origin, and used the lack of observed parallax to argue that it was in the sphere of fixed stars, further undermining the doctrine of the immutability of the heavens (the idea accepted since Aristotle that the celestial spheres were perfect and unchanging). The birth of a new star implied the variability of the heavens. In an appendix, Kepler also discussed the recent chronology work of the Polish historian Laurentius Suslyga; he calculated that, if Suslyga was correct that accepted timelines were four years behind, then the Star of Bethlehem — analogous to the present new star — would have coincided with the first great conjunction of the earlier 800 year cycle.

The extended line of research that culminated in Astronomia nova (A New Astronomy) — including the first two laws of planetary motion — began with the analysis, under Tycho's direction, of Mars' orbit. Kepler calculated and recalculated various approximations of Mars' orbit using an equant (the mathematical tool that Copernicus had eliminated with his system), eventually creating a model that generally agreed with Tycho's observations to within two arcminutes (the average measurement error). But he was not satisfied with the complex and still slightly inaccurate result; at certain points the model differed from the data by up to eight arcminutes. The wide array of traditional mathematical astronomy methods having failed him, Kepler set about trying to fit an ovoid orbit to the data.

Within Kepler's religious view of the cosmos, the Sun (a symbol of God the Father) was the source of motive force in the solar system. As a physical basis, Kepler drew by analogy on William Gilbert's theory of the magnetic soul of the Earth from De Magnete (1600) and on his own work on optics. Kepler supposed that the motive power (or motive species) radiated by the Sun weakens with distance, causing faster or slower motion as planets move closer or farther from it. Perhaps this assumption entailed a mathematical relationship that would restore astronomical order. Based on measurements of the aphelion and perihelion of the Earth and Mars, he created a formula in which a planet's rate of motion is inversely proportional to its distance from the Sun. Verifying this relationship throughout the orbital cycle, however, required very extensive calculation; to simplify this task, by late 1602 Kepler reformulated the proportion in terms of geometry: planets sweep out equal areas in equal times — Kepler's second law of planetary motion.

He then set about calculating the entire orbit of Mars, using the geometrical rate law and assuming an egg shaped ovoid orbit. After approximately 40 failed attempts, in early 1605 he at last hit upon the idea of an ellipse, which he had previously assumed to be too simple a solution for earlier astronomers to have overlooked. Finding that an elliptical orbit fit the Mars data, he immediately concluded that all planets move in ellipses, with the sun at one focus — Kepler's first law of planetary motion. Because he employed no calculating assistants, however, he did not extend the mathematical analysis beyond Mars. By the end of the year, he completed the manuscript for Astronomia nova, though it would not be published until 1609 due to legal disputes over the use of Tycho's observations, the property of his heirs.

In the years following the completion of Astronomia Nova, most of Kepler's research was focused on preparations for the Rudolphine Tables and a comprehensive set of ephemerides (specific predictions of planet and star positions) based on the table (though neither would be completed for many years). He also attempted (unsuccessfully) to begin a collaboration with Italian astronomer Giovanni Antonio Magini. Some of his other work dealt with chronology, especially the dating of events in the life of Jesus, and with astrology, especially criticism of dramatic predictions of catastrophe such as those of Helisaeus Roeslin.

Kepler and Roeslin engaged in series of published attacks and counter - attacks, while physician Philip Feselius published a work dismissing astrology altogether (and Roeslin's work in particular). In response to what Kepler saw as the excesses of astrology on the one hand and overzealous rejection of it on the other, Kepler prepared Tertius Interveniens (Third - party Interventions). Nominally this work — presented to the common patron of Roeslin and Feselius — was a neutral mediation between the feuding scholars, but it also set out Kepler's general views on the value of astrology, including some hypothesized mechanisms of interaction between planets and individual souls. While Kepler considered most traditional rules and methods of astrology to be the "evil - smelling dung" in which "an industrious hen" scrapes, there was "also perhaps a good little grain" to be found by the conscientious scientific astrologer.

In the first months of 1610, Galileo Galilei — using his powerful new telescope — discovered four satellites orbiting Jupiter. Upon publishing his account as Sidereus Nuncius (Starry Messenger), Galileo sought the opinion of Kepler, in part to bolster the credibility of his observations. Kepler responded enthusiastically with a short published reply, Dissertatio cum Nuncio Sidereo (Conversation with the Starry Messenger). He endorsed Galileo's observations and offered a range of speculations about the meaning and implications of Galileo's discoveries and telescopic methods, for astronomy and optics as well as cosmology and astrology. Later that year, Kepler published his own telescopic observations of the moons in Narratio de Jovis Satellitibus, providing further support of Galileo. To Kepler's disappointment, however, Galileo never published his reactions (if any) to Astronomia Nova.

After hearing of Galileo's telescopic discoveries, Kepler also started a theoretical and experimental investigation of telescopic optics using a telescope borrowed from Duke Ernest of Cologne. The resulting manuscript was completed in September 1610 and published as Dioptrice in 1611. In it, Kepler set out the theoretical basis of double - convex converging lenses and double - concave diverging lenses — and how they are combined to produce a Galilean telescope — as well as the concepts of real vs. virtual images, upright vs. inverted images, and the effects of focal length on magnification and reduction. He also described an improved telescope — now known as the astronomical or Keplerian telescope — in which two convex lenses can produce higher magnification than Galileo's combination of convex and concave lenses.

Around 1611, Kepler circulated a manuscript of what would eventually be published (posthumously) as Somnium (The Dream). Part of the purpose of Somnium was to describe what practicing astronomy would be like from the perspective of another planet, to show the feasibility of a non - geocentric system. The manuscript, which disappeared after changing hands several times, described a fantastic trip to the moon; it was part allegory, part autobiography, and part treatise on interplanetary travel (and is sometimes described as the first work of science fiction). Years later, a distorted version of the story may have instigated the witchcraft trial against his mother, as the mother of the narrator consults a demon to learn the means of space travel. Following her eventual acquittal, Kepler composed 223 footnotes to the story — several times longer than the actual text — which explained the allegorical aspects as well as the considerable scientific content (particularly regarding lunar geography) hidden within the text.

As a New Year's gift that year, he also composed for his friend and some time patron Baron Wackher von Wackhenfels a short pamphlet entitled Strena Seu de Nive Sexangula (A New Year's Gift of Hexagonal Snow). In this treatise, he published the first description of the hexagonal symmetry of snowflakes and, extending the discussion into a hypothetical atomistic physical basis for the symmetry and posed what later became known as the Kepler conjecture, a statement about the most efficient arrangement for packing spheres. Kepler was one of the pioneers of the mathematical applications of infinitesimals.

In 1611, the growing political - religious tension in Prague came to a head. Emperor Rudolph — whose health was failing — was forced to abdicate as King of Bohemia by his brother Matthias. Both sides sought Kepler's astrological advice, an opportunity he used to deliver conciliatory political advice (with little reference to the stars, except in general statements to discourage drastic action). However, it was clear that Kepler's future prospects in the court of Matthias were dim.

Also in that year, Barbara Kepler contracted Hungarian spotted fever, then began having seizures. As Barbara was recovering, Kepler's three children all fell sick with smallpox; Friedrich, 6, died. Following his son's death, Kepler sent letters to potential patrons in Württemberg and Padua. At the University of Tübingen in Württemberg, concerns over Kepler's perceived Calvinist heresies in violation of the Augsburg Confession and the Formula of Concord prevented his return. The University of Padua — on the recommendation of the departing Galileo — sought Kepler to fill the mathematics professorship, but Kepler, preferring to keep his family in German territory, instead traveled to Austria to arrange a position as teacher and district mathematician in Linz. However, Barbara relapsed into illness and died shortly after Kepler's return.

Kepler postponed the move to Linz and remained in Prague until Rudolph's death in early 1612, though between political upheaval, religious tension, and family tragedy (along with the legal dispute over his wife's estate), Kepler could do no research. Instead, he pieced together a chronology manuscript, Eclogae Chronicae, from correspondence and earlier work. Upon succession as Holy Roman Emperor, Matthias re-affirmed Kepler's position (and salary) as imperial mathematician but allowed him to move to Linz.

In Linz, Kepler's primary responsibilities (beyond completing the Rudolphine Tables) were teaching at the district school and providing astrological and astronomical services. In his first years there, he enjoyed financial security and religious freedom relative to his life in Prague — though he was excluded from Eucharist by his Lutheran church over his theological scruples. His first publication in Linz was De vero Anno (1613), an expanded treatise on the year of Christ's birth; he also participated in deliberations on whether to introduce Pope Gregory's reformed calendar to Protestant German lands; that year he also wrote the influential mathematical treatise Nova stereometria doliorum vinariorum, on measuring the volume of containers such as wine barrels, published in 1615.

On October 30, 1613, Kepler married the 24 year old Susanna Reuttinger. Following the death of his first wife Barbara, Kepler had considered 11 different matches. He eventually returned to Reuttinger (the fifth match) who, he wrote, "won me over with love, humble loyalty, economy of household, diligence, and the love she gave the stepchildren." The first three children of this marriage (Margareta Regina, Katharina, and Sebald) died in childhood. Three more survived into adulthood: Cordula (b. 1621); Fridmar (b. 1623); and Hildebert (b. 1625). According to Kepler's biographers, this was a much happier marriage than his first.

Since completing the Astronomia nova, Kepler had intended to compose an astronomy textbook. In 1615, he completed the first of three volumes of Epitome astronomiae Copernicanae (Epitome of Copernican Astronomy); the first volume (books I-III) was printed in 1617, the second (book IV) in 1620, and the third (books V-VII) in 1621. Despite the title, which referred simply to heliocentrism, Kepler's textbook culminated in his own ellipse based system. The Epitome became Kepler's most influential work. It contained all three laws of planetary motion and attempted to explain heavenly motions through physical causes. Though it explicitly extended the first two laws of planetary motion (applied to Mars in Astronomia nova) to all the planets as well as the Moon and the Medicean satellites of Jupiter, it did not explain how elliptical orbits could be derived from observational data.

As a spin - off from the Rudolphine Tables and the related Ephemerides, Kepler published astrological calendars, which were very popular and helped offset the costs of producing his other work — especially when support from the Imperial treasury was withheld. In his calendars — six between 1617 and 1624 — Kepler forecast planetary positions and weather as well as political events; the latter were often cannily accurate, thanks to his keen grasp of contemporary political and theological tensions. By 1624, however, the escalation of those tensions and the ambiguity of the prophecies meant political trouble for Kepler himself; his final calendar was publicly burned in Graz.

In 1615, Ursula Reingold, a woman in a financial dispute with Kepler's brother Christoph, claimed Kepler's mother Katharina had made her sick with an evil brew. The dispute escalated, and in 1617, Katharina was accused of witchcraft; witchcraft trials were relatively common in central Europe at this time. Beginning in August 1620 she was imprisoned for fourteen months. She was released in October 1621, thanks in part to the extensive legal defense drawn up by Kepler. The accusers had no stronger evidence than rumors, along with a distorted, second hand version of Kepler's Somnium, in which a woman mixes potions and enlists the aid of a demon. Katharina was subjected to territio verbalis, a graphic description of the torture awaiting her as a witch, in a final attempt to make her confess. Throughout the trial, Kepler postponed his other work to focus on his "harmonic theory". The result, published in 1619, was Harmonices Mundi ("Harmony of the World").

Kepler was convinced "that the geometrical things have provided the Creator with the model for decorating the whole world." In Harmony, he attempted to explain the proportions of the natural world — particularly the astronomical and astrological aspects — in terms of music. The central set of "harmonies" was the musica universalis or "music of the spheres," which had been studied by Pythagoras, Ptolemy and many others before Kepler; in fact, soon after publishing Harmonices Mundi, Kepler was embroiled in a priority dispute with Robert Fludd, who had recently published his own harmonic theory.

Kepler began by exploring regular polygons and regular solids, including the figures that would come to be known as Kepler's solids. From there, he extended his harmonic analysis to music, meteorology and astrology; harmony resulted from the tones made by the souls of heavenly bodies — and in the case of astrology, the interaction between those tones and human souls. In the final portion of the work (Book V), Kepler dealt with planetary motions, especially relationships between orbital velocity and orbital distance from the Sun. Similar relationships had been used by other astronomers, but Kepler — with Tycho's data and his own astronomical theories — treated them much more precisely and attached new physical significance to them.

Among many other harmonies, Kepler articulated what came to be known as the third law of planetary motion. He then tried many combinations until he discovered that (approximately) "The square of the periodic times are to each other as the cubes of the mean distances." Although he gives the date of this epiphany (March 8, 1618), he does not give any details about how he arrived at this conclusion. However, the wider significance for planetary dynamics of this purely kinematical law was not realized until the 1660s. For when conjoined with Christian Huygens' newly discovered law of centrifugal force it enabled Isaac Newton, Edmund Halley and perhaps Christopher Wren and Robert Hooke to demonstrate independently that the presumed gravitational attraction between the Sun and its planets decreased with the square of the distance between them. This refuted the traditional assumption of scholastic physics that the power of gravitational attraction remained constant with distance whenever it applied between two bodies, such as was assumed by Kepler and also by Galileo in his mistaken universal law that gravitational fall is uniformly accelerated, and also by Galileo's student Borrelli in his 1666 celestial mechanics. William Gilbert, after experimenting with magnets decided that the center of the Earth was a huge magnet. His theory led Kepler to think that a magnetic force from the Sun drove planets in their own orbits. It was an interesting explanation for planetary motion, but it was wrong. Before scientists could find the right answer, they needed to know more about motion.

In 1623, Kepler at last completed the Rudolphine Tables, which at the time was considered his major work. However, due to the publishing requirements of the emperor and negotiations with Tycho Brahe's heir, it would not be printed until 1627. In the meantime religious tension — the root of the ongoing Thirty Years' War — once again put Kepler and his family in jeopardy. In 1625, agents of the Catholic Counter - Reformation placed most of Kepler's library under seal, and in 1626 the city of Linz was besieged. Kepler moved to Ulm, where he arranged for the printing of the Tables at his own expense.

In 1628, following the military successes of the Emperor Ferdinand's armies under General Wallenstein, Kepler became an official advisor to Wallenstein. Though not the general's court astrologer per se, Kepler provided astronomical calculations for Wallenstein's astrologers and occasionally wrote horoscopes himself. In his final years, Kepler spent much of his time traveling, from the imperial court in Prague to Linz and Ulm to a temporary home in Sagan, and finally to Regensburg. Soon after arriving in Regensburg, Kepler fell ill. He died on November 15, 1630, and was buried there; his burial site was lost after the Swedish army destroyed the churchyard. Only Kepler's self - authored poetic epitaph survived the times:

Mensus eram coelos, nunc terrae metior umbras

Mens coelestis erat, corporis umbra iacet.

I measured the skies, now the shadows I measure

Skybound was the mind, earthbound the body rests.

Kepler's laws were not immediately accepted. Several major figures such as Galileo and René Descartes completely ignored Kepler's Astronomia nova. Many astronomers, including Kepler's teacher, Michael Maestlin, objected to Kepler's introduction of physics into his astronomy. Some adopted compromise positions. Ismael Boulliau accepted elliptical orbits but replaced Kepler's area law with uniform motion in respect to the empty focus of the ellipse while Seth Ward used an elliptical orbit with motions defined by an equant.

Several astronomers tested Kepler's theory, and its various modifications, against astronomical observations. Two transits of Venus and Mercury across the face of the sun provided sensitive tests of the theory, under circumstances when these planets could not normally be observed. In the case of the transit of Mercury in 1631, Kepler had been extremely uncertain of the parameters for Mercury, and advised observers to look for the transit the day before and after the predicted date. Pierre Gassendi observed the transit on the date predicted, a confirmation of Kepler's prediction. This was the first observation of a transit of Mercury. However, his attempt to observe the transit of Venus just one month later, was unsuccessful due to inaccuracies in the Rudolphine Tables. Gassendi did not realize that it was not visible from most of Europe, including Paris. Jeremiah Horrocks, who observed the 1639 Venus transit, had used his own observations to adjust the parameters of the Keplerian model, predicted the transit, and then built apparatus to observe the transit. He remained a firm advocate of the Keplerian model.

Epitome of Copernican Astronomy was read by astronomers throughout Europe, and following Kepler's death it was the main vehicle for spreading Kepler's ideas. Between 1630 and 1650, it was the most widely used astronomy textbook, winning many converts to ellipse based astronomy. However, few adopted his ideas on the physical basis for celestial motions. In the late 17th century, a number of physical astronomy theories drawing from Kepler's work — notably those of Giovanni Alfonso Borelli and Robert Hooke — began to incorporate attractive forces (though not the quasi - spiritual motive species postulated by Kepler) and the Cartesian concept of inertia. This culminated in Isaac Newton's Principia Mathematica (1687), in which Newton derived Kepler's laws of planetary motion from a force - based theory of universal gravitation.

Beyond his role in the historical development of astronomy and natural philosophy, Kepler has loomed large in the philosophy and historiography of science. Kepler and his laws of motion were central to early histories of astronomy such as Jean Etienne Montucla’s 1758 Histoire des mathématiques and Jean - Baptiste Delambre's 1821 Histoire de l’astronomie moderne. These and other histories written from an Enlightenment perspective treated Kepler's metaphysical and religious arguments with skepticism and disapproval, but later Romantic era natural philosophers viewed these elements as central to his success. William Whewell, in his influential History of the Inductive Sciences of 1837, found Kepler to be the archetype of the inductive scientific genius; in his Philosophy of the Inductive Sciences of 1840, Whewell held Kepler up as the embodiment of the most advanced forms of scientific method. Similarly, Ernst Friedrich Apelt — the first to extensively study Kepler's manuscripts, after their purchase by Catherine the Great — identified Kepler as a key to the "Revolution of the sciences". Apelt, who saw Kepler's mathematics, aesthetic sensibility, physical ideas, and theology as part of a unified system of thought, produced the first extended analysis of Kepler's life and work.

Modern translations of a number of Kepler's books appeared in the late nineteenth and early twentieth centuries, the systematic publication of his collected works began in 1937 (and is nearing completion in the early 21st century), and Max Caspar's Kepler biography was published in 1948. However, Alexandre Koyré's work on Kepler was, after Apelt, the first major milestone in historical interpretations of Kepler's cosmology and its influence. In the 1930s and 1940s Koyré, and a number of others in the first generation of professional historians of science, described the "Scientific Revolution" as the central event in the history of science, and Kepler as a (perhaps the) central figure in the revolution. Koyré placed Kepler's theorization, rather than his empirical work, at the center of the intellectual transformation from ancient to modern world views. Since the 1960s, the volume of historical Kepler scholarship has expanded greatly, including studies of his astrology and meteorology, his geometrical methods, the role of his religious views in his work, his literary and rhetorical methods, his interaction with the broader cultural and philosophical currents of his time, and even his role as an historian of science.

The debate over Kepler's place in the Scientific Revolution has also produced a wide variety of philosophical and popular treatments. One of the most influential is Arthur Koestler's 1959 The Sleepwalkers, in which Kepler is unambiguously the hero (morally and theologically as well as intellectually) of the revolution. Influential philosophers of science — such as Charles Sanders Peirce, Norwood Russell Hanson, Stephen Toulmin, and Karl Popper — have repeatedly turned to Kepler: examples of incommensurability, analogical reasoning, falsification, and many other philosophical concepts have been found in Kepler's work. Physicist Wolfgang Pauli even used Kepler's priority dispute with Robert Fludd to explore the implications of analytical psychology on scientific investigation. A well received, if fanciful, historical novel by John Banville, Kepler (1981), explored many of the themes developed in Koestler's non - fiction narrative and in the philosophy of science. Somewhat more fanciful is a recent work of nonfiction, Heavenly Intrigue (2004), suggesting that Kepler murdered Tycho Brahe to gain access to his data. Kepler has acquired a popular image as an icon of scientific modernity and a man before his time; science popularizer Carl Sagan described him as "the first astrophysicist and the last scientific astrologer."

In Austria, Johannes Kepler left behind such a historical legacy that he was one of the motifs of a silver collector's coin: the 10 euro Johannes Kepler silver coin, minted on September 10, 2002. The reverse side of the coin has a portrait of Kepler, who spent some time teaching in Graz and the surrounding areas. Kepler was acquainted with Prince Hans Ulrich von Eggenberg personally, and he probably influenced the construction of Eggenberg Castle (the motif of the obverse of the coin). In front of him on the coin is the model of nested spheres and polyhedra from Mysterium Cosmographicum.

In 2009, NASA named the Kepler Mission for Kepler's contributions to the field of astronomy.

In New Zealand's Fiordland National Park there is also a range of Mountains Named after Kepler, called the Kepler Mountains and a Three Day Walking Trail known as the Kepler Track through the Mountains of the same name.

Kepler is honored together with Nicolaus Copernicus with a feast day on the liturgical calendar of the Episcopal Church (USA) on May 23.

Sir Isaac Newton PRS (25 December 1642 – 20 March 1727 [NS: 4 January 1643 – 31 March 1727]) was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."

His monograph Philosophiæ Naturalis Principia Mathematica, published in 1687, lays the foundations for most of classical mechanics. In this work, Newton described universal gravitation and the three laws of motion, which dominated the scientific view of the physical universe for the next three centuries. Newton showed that the motions of objects on Earth and of celestial bodies are governed by the same set of natural laws, by demonstrating the consistency between Kepler's laws of planetary motion and his theory of gravitation, thus removing the last doubts about heliocentrism and advancing the Scientific Revolution. The Principia is generally considered to be one of the most important scientific books ever written, due, independently, to the specific physical laws the work successfully described, and for the style of the work, which assisted in setting standards for scientific publication down to the present time.

Newton built the first practical reflecting telescope and developed a theory of color based on the observation that a prism decomposes white light into the many colors that form the visible spectrum. He also formulated an empirical law of cooling and studied the speed of sound.

In mathematics, Newton shares the credit with Gottfried Leibniz for the development of differential and integral calculus. He also demonstrated the generalized binomial theorem, developed Newton's method for approximating the roots of a function, and contributed to the study of power series.

Newton was also highly religious. He was an unorthodox Christian, and wrote more on Biblical hermeneutics and occult studies than on science and mathematics, the subjects he is mainly associated with. Newton secretly rejected Trinitarianism, fearing to be accused of refusing holy orders.

Isaac Newton was born on what is retroactively considered 4 January 1643 [OS: 25 December 1642] at Woolsthorpe Manor in Woolsthorpe - by - Colsterworth, a hamlet in the county of Lincolnshire. At the time of Newton's birth, England had not adopted the Gregorian calendar and therefore his date of birth was recorded as Christmas Day, 25 December 1642. Newton was born three months after the death of his father, a prosperous farmer also named Isaac Newton. Born prematurely, he was a small child; his mother Hannah Ayscough reportedly said that he could have fit inside a quart mug (≈ 1.1 liters). When Newton was three, his mother remarried and went to live with her new husband, the Reverend Barnabus Smith, leaving her son in the care of his maternal grandmother, Margery Ayscough. The young Isaac disliked his stepfather and held some enmity towards his mother for marrying him, as revealed by this entry in a list of sins committed up to the age of 19: "Threatening my father and mother Smith to burn them and the house over them." While Newton was once engaged in his late teens to a Miss Storey, he never married, being highly engrossed in his studies and work.

From the age of about twelve until he was seventeen, Newton was educated at The King's School, Grantham (where his alleged signature can still be seen upon a library window sill). He was removed from school, and by October 1659, he was to be found at Woolsthorpe - by - Colsterworth, where his mother, widowed by now for a second time, attempted to make a farmer of him. He hated farming. Henry Stokes, master at the King's School, persuaded his mother to send him back to school so that he might complete his education. Motivated partly by a desire for revenge against a schoolyard bully, he became the top ranked student. The Cambridge psychologist Simon Baron - Cohen considers it "fairly certain" that Newton suffered from Asperger syndrome.

In June 1661, he was admitted to Trinity College, Cambridge as a sizar – a sort of work - study role. At that time, the college's teachings were based on those of Aristotle, but Newton preferred to read the more advanced ideas of modern philosophers, such as Descartes, and of astronomers such as Copernicus, Galileo, and Kepler. In 1665, he discovered the generalized binomial theorem and began to develop a mathematical theory that later became infinitesimal calculus. Soon after Newton had obtained his degree in August 1665, the university temporarily closed as a precaution against the Great Plague. Although he had been undistinguished as a Cambridge student, Newton's private studies at his home in Woolsthorpe over the subsequent two years saw the development of his theories on calculus, optics and the law of gravitation. In 1667, he returned to Cambridge as a fellow of Trinity. Fellows were required to become ordained priests, something Newton desired to avoid due to his unorthodox views. Luckily for Newton, there was no specific deadline for ordination and it could be postponed indefinitely. The problem became more severe later when Newton was elected for the prestigious Lucasian Chair. For such a significant appointment, ordaining normally could not be dodged. Nevertheless, Newton managed to avoid it by means of a special permission from Charles II.

Newton's work has been said "to distinctly advance every branch of mathematics then studied".

His work on the subject usually referred to as fluxions or calculus is seen, for example, in a manuscript of October 1666, now published among Newton's mathematical papers. A related subject was infinite series. Newton's manuscript "De analysi per aequationes numero terminorum infinitas" ("On analysis by equations infinite in number of terms") was sent by Isaac Barrow to John Collins in June 1669: in August 1669 Barrow identified its author to Collins as "Mr Newton, a fellow of our College, and very young ... but of an extraordinary genius and proficiency in these things".

Newton later became involved in a dispute with Leibniz over priority in the development of infinitesimal calculus. Most modern historians believe that Newton and Leibniz developed infinitesimal calculus independently, although with very different notations. Occasionally it has been suggested that Newton published almost nothing about it until 1693, and did not give a full account until 1704, while Leibniz began publishing a full account of his methods in 1684. (Leibniz's notation and "differential Method", nowadays recognized as much more convenient notations, were adopted by continental European mathematicians, and after 1820 or so, also by British mathematicians.) Such a suggestion, however, fails to notice the content of calculus which critics of Newton's time and modern times have pointed out in Book 1 of Newton's Principia itself (published 1687) and in its forerunner manuscripts, such as De motu corporum in gyrum ("On the motion of bodies in orbit"), of 1684. The Principia is not written in the language of calculus either as we know it or as Newton's (later) 'dot' notation would write it. But his work extensively uses an infinitesimal calculus in geometric form, based on limiting values of the ratios of vanishing small quantities: in the Principia itself Newton gave demonstration of this under the name of 'the method of first and last ratios' and explained why he put his expositions in this form, remarking also that 'hereby the same thing is performed as by the method of indivisibles'.

Because of this, the Principia has been called "a book dense with the theory and application of the infinitesimal calculus" in modern times and "lequel est presque tout de ce calcul" ('nearly all of it is of this calculus') in Newton's time. His use of methods involving "one or more orders of the infinitesimally small" is present in his De motu corporum in gyrum of 1684 and in his papers on motion "during the two decades preceding 1684".

Newton had been reluctant to publish his calculus because he feared controversy and criticism. He had a very close relationship with Swiss mathematician Nicolas Fatio de Duillier, who from the beginning was impressed by Newton's gravitational theory. In 1691, Duillier planned to prepare a new version of Newton's Principia, but never finished it. However, in 1693 the relationship between the two men changed. At the time, Duillier had also exchanged several letters with Leibniz.

Starting in 1699, other members of the Royal Society (of which Newton was a member) accused Leibniz of plagiarism, and the dispute broke out in full force in 1711. The Royal Society proclaimed in a study that it was Newton who was the true discoverer and labeled Leibniz a fraud. This study was cast into doubt when it was later found that Newton himself wrote the study's concluding remarks on Leibniz. Thus began the bitter controversy which marred the lives of both Newton and Leibniz until the latter's death in 1716.

Newton is generally credited with the generalized binomial theorem, valid for any exponent. He discovered Newton's identities, Newton's method, classified cubic plane curves (polynomials of degree three in two variables), made substantial contributions to the theory of finite differences, and was the first to use fractional indices and to employ coordinate geometry to derive solutions to Diophantine equations. He approximated partial sums of the harmonic series by logarithms (a precursor to Euler's summation formula), and was the first to use power series with confidence and to revert power series.

He was appointed Lucasian Professor of Mathematics in 1669 on Barrow's recommendation. In that day, any fellow of Cambridge or Oxford was required to become an ordained Anglican priest. However, the terms of the Lucasian professorship required that the holder not be active in the church (presumably so as to have more time for science). Newton argued that this should exempt him from the ordination requirement, and Charles II, whose permission was needed, accepted this argument. Thus a conflict between Newton's religious views and Anglican orthodoxy was averted.

From 1670 to 1672, Newton lectured on optics. During this period he investigated the refraction of light, demonstrating that a prism could decompose white light into a spectrum of colors, and that a lens and a second prism could recompose the multicolored spectrum into white light.

He also showed that the colored light does not change its properties by separating out a colored beam and shining it on various objects. Newton noted that regardless of whether it was reflected or scattered or transmitted, it stayed the same color. Thus, he observed that color is the result of objects interacting with already colored light rather than objects generating the color themselves. This is known as Newton's theory of color.

From this work, he concluded that the lens of any refracting telescope would suffer from the dispersion of light into colours (chromatic aberration). As a proof of the concept, he constructed a telescope using a mirror as the objective to bypass that problem. Building the design, the first known functional reflecting telescope, today known as a Newtonian telescope, involved solving the problem of a suitable mirror material and shaping technique. Newton ground his own mirrors out of a custom composition of highly reflective speculum metal, using Newton's rings to judge the quality of the optics for his telescopes. In late 1668 he was able to produce this first reflecting telescope. In 1671, the Royal Society asked for a demonstration of his reflecting telescope. Their interest encouraged him to publish his notes On Colour, which he later expanded into his Opticks. When Robert Hooke criticised some of Newton's ideas, Newton was so offended that he withdrew from public debate. Newton and Hooke had brief exchanges in 1679 – 80, when Hooke, appointed to manage the Royal Society's correspondence, opened up a correspondence intended to elicit contributions from Newton to Royal Society transactions, which had the effect of stimulating Newton to work out a proof that the elliptical form of planetary orbits would result from a centripetal force inversely proportional to the square of the radius vector (Newton's law of universal gravitation – History and De motu corporum in gyrum). But the two men remained generally on poor terms until Hooke's death.

Newton argued that light is composed of particles or corpuscles, which were refracted by accelerating into a denser medium. He verged on soundlike waves to explain the repeated pattern of reflection and transmission by thin films (Opticks Bk.II, Props. 12), but still retained his theory of ‘fits’ that disposed corpuscles to be reflected or transmitted (Props.13). Later physicists instead favored a purely wavelike explanation of light to account for the interference patterns, and the general phenomenon of diffraction. Today's quantum mechanics, photons and the idea of wave – particle duality bear only a minor resemblance to Newton's understanding of light.

In his Hypothesis of Light of 1675, Newton posited the existence of the ether to transmit forces between particles. The contact with the theosophist Henry More, revived his interest in alchemy. He replaced the ether with occult forces based on Hermetic ideas of attraction and repulsion between particles. John Maynard Keynes, who acquired many of Newton's writings on alchemy, stated that "Newton was not the first of the age of reason: He was the last of the magicians." Newton's interest in alchemy cannot be isolated from his contributions to science; however, he did apparently abandon his alchemical researches. (This was at a time when there was no clear distinction between alchemy and science.) Had he not relied on the occult idea of action at a distance, across a vacuum, he might not have developed his theory of gravity.

In 1704, Newton published Opticks, in which he expounded his corpuscular theory of light. He considered light to be made up of extremely subtle corpuscles, that ordinary matter was made of grosser corpuscles and speculated that through a kind of alchemical transmutation "Are not gross Bodies and Light convertible into one another, ...and may not Bodies receive much of their Activity from the Particles of Light which enter their Composition?" Newton also constructed a primitive form of a frictional electrostatic generator, using a glass globe (Optics, 8th Query).

In an article entitled "Newton, prisms, and the 'opticks' of tunable lasers it is indicated that Newton in his book Opticks was the first to show a diagram using a prism as a beam expander. In the same book he describes, via diagrams, the use of multiple prism arrays. Some 278 years after Newton's discussion, multiple prism beam expanders became central to the development of narrow line width tunable lasers. Also, the use of these prismatic beam expanders led to the multiple prism dispersion theory.

In 1679, Newton returned to his work on (celestial) mechanics, i.e., gravitation and its effect on the orbits of planets, with reference to Kepler's laws of planetary motion. This followed stimulation by a brief exchange of letters in 1679 – 80 with Hooke, who had been appointed to manage the Royal Society's correspondence, and who opened a correspondence intended to elicit contributions from Newton to Royal Society transactions. Newton's reawakening interest in astronomical matters received further stimulus by the appearance of a comet in the winter of 1680 – 1681, on which he corresponded with John Flamsteed. After the exchanges with Hooke, Newton worked out a proof that the elliptical form of planetary orbits would result from a centripetal force inversely proportional to the square of the radius vector (Newton's law of universal gravitation). Newton communicated his results to Edmond Halley and to the Royal Society in De motu corporum in gyrum, a tract written on about 9 sheets which was copied into the Royal Society's Register Book in December 1684. This tract contained the nucleus that Newton developed and expanded to form the Principia.

The Principia was published on 5 July 1687 with encouragement and financial help from Edmond Halley. In this work, Newton stated the three universal laws of motion that enabled many of the advances of the Industrial Revolution which soon followed and were not to be improved upon for more than 200 years, and are still the underpinnings of the non - relativistic technologies of the modern world. He used the Latin word gravitas (weight) for the effect that would become known as gravity, and defined the law of universal gravitation.

In the same work, Newton presented a calculus like method of geometrical analysis by 'first and last ratios', gave the first analytical determination (based on Boyle's law) of the speed of sound in air, inferred the oblateness of the spheroidal figure of the Earth, accounted for the precession of the equinoxes as a result of the Moon's gravitational attraction on the Earth's oblateness, initiated the gravitational study of the irregularities in the motion of the moon, provided a theory for the determination of the orbits of comets, and much more.

Newton made clear his heliocentric view of the solar system – developed in a somewhat modern way, because already in the mid 1680s he recognized the "deviation of the Sun" from the centre of gravity of the solar system. For Newton, it was not precisely the center of the Sun or any other body that could be considered at rest, but rather "the common centre of gravity of the Earth, the Sun and all the Planets is to be esteem'd the Centre of the World", and this center of gravity "either is at rest or moves uniformly forward in a right line" (Newton adopted the "at rest" alternative in view of common consent that the center, wherever it was, was at rest).

Newton's postulate of an invisible force able to act over vast distances led to him being criticised for introducing "occult agencies" into science. Later, in the second edition of the Principia (1713), Newton firmly rejected such criticisms in a concluding General Scholium, writing that it was enough that the phenomena implied a gravitational attraction, as they did; but they did not so far indicate its cause, and it was both unnecessary and improper to frame hypotheses of things that were not implied by the phenomena. (Here Newton used what became his famous expression Hypotheses non fingo).

With the Principia, Newton became internationally recognized. He acquired a circle of admirers, including the Swiss born mathematician Nicolas Fatio de Duillier, with whom he formed an intense relationship that lasted until 1693, when it abruptly ended, at the same time that Newton suffered a nervous breakdown.

In the 1690s, Newton wrote a number of religious tracts dealing with the literal interpretation of the Bible. Henry More's belief in the Universe and rejection of Cartesian dualism may have influenced Newton's religious ideas. A manuscript he sent to John Locke in which he disputed the existence of the Trinity was never published. Later works – The Chronology of Ancient Kingdoms Amended (1728) and Observations Upon the Prophecies of Daniel and the Apocalypse of St. John (1733) – were published after his death. He also devoted a great deal of time to alchemy.

Newton was also a member of the Parliament of England from 1689 to 1690 and in 1701, but according to some accounts his only comments were to complain about a cold draught in the chamber and request that the window be closed.

Newton moved to London to take up the post of warden of the Royal Mint in 1696, a position that he had obtained through the patronage of Charles Montagu, 1st Earl of Halifax, then Chancellor of the Exchequer. He took charge of England's great recoining, somewhat treading on the toes of Lord Lucas, Governor of the Tower (and securing the job of deputy comptroller of the temporary Chester branch for Edmond Halley). Newton became perhaps the best known Master of the Mint upon the death of Thomas Neale in 1699, a position Newton held until his death. These appointments were intended as sinecures, but Newton took them seriously, retiring from his Cambridge duties in 1701, and exercising his power to reform the currency and punish clippers and counterfeiters. As Master of the Mint in 1717 in the "Law of Queen Anne" Newton moved the Pound Sterling de facto from the silver standard to the gold standard by setting the bimetallic relationship between gold coins and the silver penny in favor of gold. This caused silver sterling coin to be melted and shipped out of Britain. Newton was made President of the Royal Society in 1703 and an associate of the French Académie des Sciences. In his position at the Royal Society, Newton made an enemy of John Flamsteed, the Astronomer Royal, by prematurely publishing Flamsteed's Historia Coelestis Britannica, which Newton had used in his studies.

In April 1705, Queen Anne knighted Newton during a royal visit to Trinity College, Cambridge. The knighthood is likely to have been motivated by political considerations connected with the Parliamentary election in May 1705, rather than any recognition of Newton's scientific work or services as Master of the Mint. Newton was the second scientist to be knighted, after Sir Francis Bacon.

Towards the end of his life, Newton took up residence at Cranbury Park, near Winchester with his niece and her husband, until his death in 1727. Newton died in his sleep in London on 31 March 1727 [OS: 20 March 1726], and was buried in Westminster Abbey. His half - niece, Catherine Barton Conduitt, served as his hostess in social affairs at his house on Jermyn Street in London; he was her "very loving Uncle," according to his letter to her when she was recovering from smallpox. Newton, a bachelor, had divested much of his estate to relatives during his last years, and died intestate.

After his death, Newton's body was discovered to have had massive amounts of mercury in it, probably resulting from his alchemical pursuits. Mercury poisoning could explain Newton's eccentricity in late life.

French mathematician Joseph - Louis Lagrange often said that Newton was the greatest genius who ever lived, and once added that Newton was also "the most fortunate, for we cannot find more than once a system of the world to establish." English poet Alexander Pope was moved by Newton's accomplishments to write the famous epitaph:

Nature and nature's laws lay hid in night;
God said "Let Newton be" and all was light.

Newton himself had been rather more modest of his own achievements, famously writing in a letter to Robert Hooke in February 1676:

If I have seen further it is by standing on the shoulders of giants.

Two writers think that the above quote, written at a time when Newton and Hooke were in dispute over optical discoveries, was an oblique attack on Hooke (said to have been short and hunchbacked), rather than – or in addition to – a statement of modesty. On the other hand, the widely known proverb about standing on the shoulders of giants published among others by 17th century poet George Herbert (a former orator of the University of Cambridge and fellow of Trinity College) in his Jacula Prudentum (1651), had as its main point that "a dwarf on a giant's shoulders sees farther of the two", and so its effect as an analogy would place Newton himself rather than Hooke as the 'dwarf'.

In a later memoir, Newton wrote:

I do not know what I may appear to the world, but to myself I seem to have been only like a boy playing on the sea - shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me.

Albert Einstein kept a picture of Newton on his study wall alongside ones of Michael Faraday and James Clerk Maxwell. Newton remains influential to today's scientists, as demonstrated by a 2005 survey of members of Britain's Royal Society (formerly headed by Newton) asking who had the greater effect on the history of science, Newton or Einstein. Royal Society scientists deemed Newton to have made the greater overall contribution. In 1999, an opinion poll of 100 of today's leading physicists voted Einstein the "greatest physicist ever;" with Newton the runner-up, while a parallel survey of rank - and - file physicists by the site PhysicsWeb gave the top spot to Newton.

Newton's monument (1731) can be seen in Westminster Abbey, at the north of the entrance to the choir against the choir screen, near his tomb. It was executed by the sculptor Michael Rysbrack (1694 – 1770) in white and grey marble with design by the architect William Kent. The monument features a figure of Newton reclining on top of a sarcophagus, his right elbow resting on several of his great books and his left hand pointing to a scroll with a mathematical design. Above him is a pyramid and a celestial globe showing the signs of the Zodiac and the path of the comet of 1680. A relief panel depicts putti using instruments such as a telescope and prism. The Latin inscription on the base translates as:

Here is buried Isaac Newton, Knight, who by a strength of mind almost divine, and mathematical principles peculiarly his own, explored the course and figures of the planets, the paths of comets, the tides of the sea, the dissimilarities in rays of light, and, what no other scholar has previously imagined, the properties of the colors thus produced. Diligent, sagacious and faithful, in his expositions of nature, antiquity and the holy Scriptures, he vindicated by his philosophy the majesty of God mighty and good, and expressed the simplicity of the Gospel in his manners. Mortals rejoice that there has existed such and so great an ornament of the human race! He was born on 25 December 1642, and died on 20 March 1726/7. — Translation from G.L. Smyth, The Monuments and Genii of St. Paul's Cathedral, and of Westminster Abbey (1826), ii, 703–4.

From 1978 until 1988, an image of Newton designed by Harry Ecclestone appeared on Series D £1 banknotes issued by the Bank of England (the last £1 notes to be issued by the Bank of England). Newton was shown on the reverse of the notes holding a book and accompanied by a telescope, a prism and a map of the Solar System.

A statue of Isaac Newton, looking at an apple at his feet, can be seen at the Oxford University Museum of Natural History.

According to most scholars, Newton was a monotheist who believed in biblical prophecies but was Antitrinitarian. 'In Newton's eyes, worshipping Christ as God was idolatry, to him the fundamental sin'. Historian Stephen D. Snobelen says of Newton, "Isaac Newton was a heretic. But ... he never made a public declaration of his private faith — which the orthodox would have deemed extremely radical. He hid his faith so well that scholars are still unravelling his personal beliefs." Snobelen concludes that Newton was at least a Socinian sympathiser (he owned and had thoroughly read at least eight Socinian books), possibly an Arian and almost certainly an anti - trinitarian. In an age notable for its religious intolerance, there are few public expressions of Newton's radical views, most notably his refusal to take holy orders and his refusal, on his death bed, to take the sacrament when it was offered to him.

In a view disputed by Snobelen, T.C. Pfizenmaier argues that Newton held the Arian view of the Trinity rather than the Western one held by Roman Catholics, Anglicans, and most Protestants.

Although the laws of motion and universal gravitation became Newton's best known discoveries, he warned against using them to view the Universe as a mere machine, as if akin to a great clock. He said, "Gravity explains the motions of the planets, but it cannot explain who set the planets in motion. God governs all things and knows all that is or can be done."

His scientific fame notwithstanding, Newton's studies of the Bible and of the early Church Fathers were also noteworthy. Newton wrote works on textual criticism, most notably An Historical Account of Two Notable Corruptions of Scripture. He also placed the crucifixion of Jesus Christ at 3 April, AD 33, which agrees with one traditionally accepted date. He also tried, unsuccessfully, to find hidden messages within the Bible.

Newton wrote more on religion than he did on natural science. He believed in a rationally immanent world, but he rejected the hylozoism implicit in Leibniz and Baruch Spinoza. Thus, the ordered and dynamically informed Universe could be understood, and must be understood, by an active reason. In his correspondence, Newton claimed that in writing the Principia "I had an eye upon such Principles as might work with considering men for the belief of a Deity". He saw evidence of design in the system of the world: "Such a wonderful uniformity in the planetary system must be allowed the effect of choice". But Newton insisted that divine intervention would eventually be required to reform the system, due to the slow growth of instabilities. For this, Leibniz lampooned him: "God Almighty wants to wind up his watch from time to time: otherwise it would cease to move. He had not, it seems, sufficient foresight to make it a perpetual motion." Newton's position was vigorously defended by his follower Samuel Clarke in a famous correspondence.

Newton and Robert Boyle's mechanical philosophy was promoted by rationalist pamphleteers as a viable alternative to the pantheists and enthusiasts, and was accepted hesitantly by orthodox preachers as well as dissident preachers like the latitudinarians. Thus, the clarity and simplicity of science was seen as a way to combat the emotional and metaphysical superlatives of both superstitious enthusiasm and the threat of atheism, and, at the same time, the second wave of English deists used Newton's discoveries to demonstrate the possibility of a "Natural Religion".

The attacks made against pre - Enlightenment "magical thinking", and the mystical elements of Christianity, were given their foundation with Boyle's mechanical conception of the Universe. Newton gave Boyle's ideas their completion through mathematical proofs and, perhaps more importantly, was very successful in popularising them. Newton refashioned the world governed by an interventionist God into a world crafted by a God that designs along rational and universal principles. These principles were available for all people to discover, allowed people to pursue their own aims fruitfully in this life, not the next, and to perfect themselves with their own rational powers.

Newton saw God as the master creator whose existence could not be denied in the face of the grandeur of all creation. His spokesman, Clarke, rejected Leibniz' theodicy which cleared God from the responsibility for l'origine du mal by making God removed from participation in his creation, since as Clarke pointed out, such a deity would be a king in name only, and but one step away from atheism. But the unforeseen theological consequence of the success of Newton's system over the next century was to reinforce the deist position advocated by Leibniz. The understanding of the world was now brought down to the level of simple human reason, and humans, as Odo Marquard argued, became responsible for the correction and elimination of evil.

In a manuscript he wrote in 1704 in which he describes his attempts to extract scientific information from the Bible, he estimated that the world would end no earlier than 2060. In predicting this he said, "This I mention not to assert when the time of the end shall be, but to put a stop to the rash conjectures of fanciful men who are frequently predicting the time of the end, and by doing so bring the sacred prophesies into discredit as often as their predictions fail."

Enlightenment philosophers chose a short history of scientific predecessors — Galileo, Boyle, and Newton principally — as the guides and guarantors of their applications of the singular concept of Nature and Natural Law to every physical and social field of the day. In this respect, the lessons of history and the social structures built upon it could be discarded.

It was Newton's conception of the Universe based upon Natural and rationally understandable laws that became one of the seeds for Enlightenment ideology. Locke and Voltaire applied concepts of Natural Law to political systems advocating intrinsic rights; the physiocrats and Adam Smith applied Natural conceptions of psychology and self - interest to economic systems; and sociologists criticised the current social order for trying to fit history into Natural models of progress. Monboddo and Samuel Clarke resisted elements of Newton's work, but eventually rationalized it to conform with their strong religious views of nature.

As warden of the Royal Mint, Newton estimated that 20 percent of the coins taken in during The Great Recoinage of 1696 were counterfeit. Counterfeiting was high treason, punishable by the felon's being hanged, drawn and quartered. Despite this, convicting the most flagrant criminals could be extremely difficult. However, Newton proved to be equal to the task. Disguised as a habitué of bars and taverns, he gathered much of that evidence himself. For all the barriers placed to prosecution, and separating the branches of government, English law still had ancient and formidable customs of authority. Newton had himself made a justice of the peace in all the home counties - there is a draft of a letter regarding this matter stuck into Newton's personal first edition of his Philosophiæ Naturalis Principia Mathematica which he must have been amending at the time. Then he conducted more than 100 cross examinations of witnesses, informers, and suspects between June 1698 and Christmas 1699. Newton successfully prosecuted 28 coiners.

One of Newton's cases as the King's attorney was against William Chaloner. Chaloner's schemes included setting up phony conspiracies of Catholics and then turning in the hapless conspirators whom he had entrapped. Chaloner made himself rich enough to posture as a gentleman. Petitioning Parliament, Chaloner accused the Mint of providing tools to counterfeiters (a charge also made by others). He proposed that he be allowed to inspect the Mint's processes in order to improve them. He petitioned Parliament to adopt his plans for a coinage that could not be counterfeited, while at the same time striking false coins. Newton put Chaloner on trial for counterfeiting and had him sent to Newgate Prison in September 1697. But Chaloner had friends in high places, who helped him secure an acquittal and his release. Newton put him on trial a second time with conclusive evidence. Chaloner was convicted of high treason and hanged, drawn and quartered on 23 March 1699 at Tyburn gallows.

The famous three laws of motion (stated in modernized form): Newton's First Law (also known as the Law of Inertia) states that an object at rest tends to stay at rest and that an object in uniform motion tends to stay in uniform motion unless acted upon by a net external force. The meaning of this law is the existence of reference frames (called inertial frames) where objects not acted upon by forces move in uniform motion (in particular, they may be at rest).

Newton's Second Law states that an applied force, 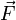, on an object equals the rate of change of its momentum, 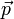, with time. Mathematically, this is expressed as

If applied to an object with constant mass (dm/dt = 0), the first term vanishes, and by substitution using the definition of acceleration, the equation can be written in the iconic form

The first and second laws represent a break with the physics of Aristotle, in which it was believed that a force was necessary in order to maintain motion. They state that a force is only needed in order to change an object's state of motion. The SI unit of force is the newton, named in Newton's honour.

Newton's Third Law states that for every action there is an equal and opposite reaction. This means that any force exerted onto an object has a counterpart force that is exerted in the opposite direction back onto the first object. A common example is of two ice skaters pushing against each other and sliding apart in opposite directions. Another example is the recoil of a firearm, in which the force propelling the bulletis exerted equally back onto the gun and is felt by the shooter. Since the objects in question do not necessarily have the same mass, the resulting acceleration of the two objects can be different (as in the case of firearm recoil).

Unlike Aristotle's, Newton's physics is meant to be universal. For example, the second law applies both to a planet and to a falling stone.

The vector nature of the second law addresses the geometrical relationship between the direction of the force and the manner in which the object's momentum changes. Before Newton, it had typically been assumed that a planet orbiting the sun would need a forward force to keep it moving. Newton showed instead that all that was needed was an inward attraction from the sun. Even many decades after the publication of the Principia, this counterintuitive idea was not universally accepted, and many scientists preferred Descartes' theory of vortices.

Newton himself often told the story that he was inspired to formulate his theory of gravitation by watching the fall of an apple from a tree. Although it has been said that the apple story is a myth and that he did not arrive at his theory of gravity in any single moment, acquaintances of Newton (such as William Stukeley, whose manuscript account, published in 1752, has been made available by the Royal Society) do in fact confirm the incident, though not the cartoon version that the apple actually hit Newton's head. Stukeley recorded in his Memoirs of Sir Isaac Newton's Life a conversation with Newton in Kensington on 15 April 1726:

... We went into the garden, & drank thea under the shade of some appletrees, only he, & myself. amidst other discourse, he told me, he was just in the same situation, as when formerly, the notion of gravitation came into his mind. "why should that apple always descend perpendicularly to the ground," thought he to him self: occasion'd by the fall of an apple, as he sat in a comtemplative mood: "why should it not go sideways, or upwards? but constantly to the earths centre? assuredly, the reason is, that the earth draws it. there must be a drawing power in matter. & the sum of the drawing power in the matter of the earth must be in the earths centre, not in any side of the earth. therefore dos this apple fall perpendicularly, or toward the centre. if matter thus draws matter; it must be in proportion of its quantity. therefore the apple draws the earth, as well as the earth draws the apple."

John Conduitt, Newton's assistant at the Royal Mint and husband of Newton's niece, also described the event when he wrote about Newton's life:

In the year 1666 he retired again from Cambridge to his mother in Lincolnshire. Whilst he was pensively meandering in a garden it came into his thought that the power of gravity (which brought an apple from a tree to the ground) was not limited to a certain distance from earth, but that this power must extend much further than was usually thought. Why not as high as the Moon said he to himself & if so, that must influence her motion & perhaps retain her in her orbit, whereupon he fell a calculating what would be the effect of that supposition.

In similar terms, Voltaire wrote in his Essay on Epic Poetry (1727), "Sir Isaac Newton walking in his gardens, had the first thought of his system of gravitation, upon seeing an apple falling from a tree."

It is known from his notebooks that Newton was grappling in the late 1660s with the idea that terrestrial gravity extends, in an inverse square proportion, to the Moon; however it took him two decades to develop the full fledged theory. The question was not whether gravity existed, but whether it extended so far from Earth that it could also be the force holding the moon to its orbit. Newton showed that if the force decreased as the inverse square of the distance, one could indeed calculate the Moon's orbital period, and get good agreement. He guessed the same force was responsible for other orbital motions, and hence named it "universal gravitation".

Various trees are claimed to be "the" apple tree which Newton describes. The King's School, Grantham, claims that the tree was purchased by the school, uprooted and transported to the headmaster's garden some years later. The staff of the [now] National Trust owned Woolsthorpe Manor dispute this, and claim that a tree present in their gardens is the one described by Newton. A descendant of the original tree can be seen growing outside the main gate of Trinity College, Cambridge, below the room Newton lived in when he studied there. The National Fruit Collection at Brogdale can supply grafts from their tree, which appears identical to Flower of Kent, a coarse fleshed cooking variety.