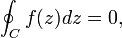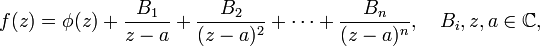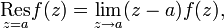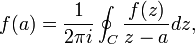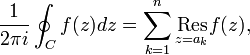• Mathematician Augustin - Louis Cauchy, 1789
• Mathematician Arthur Cayley, 1821

Baron Augustin - Louis Cauchy (21 August 1789 – 23 May 1857) was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors. He defined continuity in terms of infinitesimals and gave several important theorems in complex analysis and initiated the study of permutation groups in abstract algebra. A profound mathematician, Cauchy exercised a great influence over his contemporaries and successors. His writings cover the entire range of mathematics and mathematical physics.

Cauchy was a prolific writer; he wrote approximately eight hundred research articles and five complete textbooks. He was a devout Roman Catholic, strict Bourbon royalist, and a close associate of the Jesuit order.

Cauchy was the son of Louis François Cauchy (1760 - 1848) and Marie - Madeleine Desestre. Cauchy had two brothers, Alexandre Laurent Cauchy (1792 - 1857), who became a president of a division of the court of appeal in 1847, and a judge of the court of cassation in 1849; and Eugene Francois Cauchy (1802 - 1877), a publicist who also wrote several mathematical works.

Cauchy married Aloise de Bure in 1818. She was a close relative of the publisher who published most of Cauchy's works. By her he had two daughters, Marie Françoise Alicia (1819) and Marie Mathilde (1823).

Cauchy's father (Louis François Cauchy) was a high official in the Parisian Police of the New Régime. He lost his position because of the French Revolution (July 14, 1789) that broke out one month before Augustin - Louis was born. The Cauchy family survived the revolution and the following Reign of Terror (1794) by escaping to Arcueil, where Cauchy received his first education, from his father. After the execution of Robespierre (1794), it was safe for the family to return to Paris. There Louis - François Cauchy found himself a new bureaucratic job, and quickly moved up the ranks. When Napoleon Bonaparte came to power (1799), Louis - François Cauchy was further promoted, and became Secretary - General of the Senate, working directly under Laplace (who is now better known for his work on mathematical physics). The famous mathematician Lagrange was also no stranger in the Cauchy family.

On Lagrange's advice, Augustin - Louis was enrolled in the École Centrale du Panthéon, the best secondary school of Paris at that time, in the fall of 1802. Most of the curriculum consisted of classical languages; the young and ambitious Cauchy, being a brilliant student, won many prizes in Latin and Humanities. In spite of these successes, Augustin - Louis chose an engineering career, and prepared himself for the entrance examination to the École Polytechnique.

In 1805 he placed second out of 293 applicants on this exam, and he was admitted. One of the main purposes of this school was to give future civil and military engineers a high level scientific and mathematical education. The school functioned under military discipline, which caused the young and pious Cauchy some problems in adapting. Nevertheless, he finished the Polytechnique in 1807, at the age of 18, and went on to the École des Ponts et Chaussées (School for Bridges and Roads). He graduated in civil engineering, with the highest honors.

After finishing school in 1810, Cauchy accepted a job as a junior engineer in Cherbourg, where Napoleon intended to build a naval base. Here Augustin - Louis stayed for three years, and although he had an extremely busy managerial job, he still found time to prepare three mathematical manuscripts, which he submitted to the Première Classe (First Class) of the Institut de France. Cauchy's first two manuscripts (on polyhedra) were accepted; the third one (on directrices of conic sections) was rejected.

In September 1812, now 23 years old, after becoming ill from overwork, Cauchy returned to Paris. Another reason for his return to the capital was that he was losing his interest in his engineering job, being more and more attracted to abstract beauty of mathematics; in Paris he would have a much better chance to find a mathematics related position. Although he formally kept his engineering position, he was transferred from the payroll of the Ministry of the Marine to the Ministry of the Interior. The next three years Augustin - Louis was mainly on unpaid sick leave, and spent his time quite fruitfully, working on mathematics (on the related topics of symmetric functions, the symmetric group and the theory of higher - order algebraic equations). He attempted admission to the First Class of the Institut de France but failed on three different occasions between 1813 and 1815. In 1815 Napoleon was defeated at Waterloo, and the newly installed Bourbon king Louis XVIII (a brother of the beheaded Louis XVI) took the restoration in hand. The Académie des Sciences was re-established in March 1816; Lazare Carnot and Gaspard Monge were removed from this Academy for political reasons, and the king appointed Cauchy to take the place of one of them. The reaction by Cauchy's peers was harsh; they considered his acceptance of membership of the Academy an outrage, and Cauchy thereby created many enemies in scientific circles.

In November 1815, Louis Poinsot, who was an associate professor at the École Polytechnique, asked to be exempted from his teaching duties for health reasons. Cauchy was by then a rising mathematical star, who certainly merited a professorship. One of his great successes at that time was the proof of Fermat's polygonal number theorem. However, the fact that Cauchy was known to be very loyal to the Bourbons, doubtless also helped him in becoming the successor of Poinsot. He finally quit his engineering job, and received a one year contract for teaching mathematics to second year students of the École Polytechnique. In 1816, this Bonapartist, non - religious school was reorganized, and several liberal professors were fired; the reactionary Cauchy was promoted to full professor.

When Cauchy was 28 years old, he was still living with his parents. His father found it high time for his son to marry; he found him a suitable bride, Aloïse de Bure, five years his junior. She was a close relative of the publisher who published most of Cauchy's works. They were married on April 4, 1818, with great Roman Catholic pomp and ceremony, in the Church of Saint - Sulpice. In 1819 the couple's first daughter, Marie Françoise Alicia, was born, and in 1823 the second and last daughter, Marie Mathilde. Cauchy had two brothers: Alexandre Laurent Cauchy, who became a president of a division of the court of appeal in 1847, and a judge of the court of cassation in 1849; and Eugène François Cauchy, a publicist who also wrote several mathematical works.

The oppressive political climate that lasted until 1830 suited Cauchy perfectly. In 1824 Louis XVIII died, and was succeeded by his even more reactionary brother Charles X. During these years Cauchy was highly productive, and published one important mathematical treatise after another. He received cross appointments at the Collège de France, and the Faculté des Sciences of the University.

In July 1830 France underwent another revolution. Charles X fled the country, and was succeeded by the non - Bourbon king Louis - Philippe (of the House of Orléans). Riots, in which uniformed students of the École Polytechnique took an active part, raged close to Cauchy's home in Paris.

These events marked a turning point in Cauchy's life, and a break in his mathematical productivity. Cauchy, shaken by the fall of the government, and moved by a deep hatred of the liberals who were taking power, left Paris to go abroad, leaving his family behind. He spent a short time at Fribourg in Switzerland, where he had to decide whether he would swear a required oath of allegiance to the new regime. He refused to do this, and consequently lost all his positions in Paris, except his membership of the Academy, for which an oath was not required. In 1831 Cauchy went to the Italian city of Turin, and after some time there, he accepted an offer from the King of Sardinia (who ruled Turin and the surrounding Piedmont region) for a chair of theoretical physics, which was created especially for him. He taught in Turin during 1832 - 1833. In 1831, he had been elected a foreign member of the Royal Swedish Academy of Sciences.

In August 1833 Cauchy left Turin for Prague, to become the science tutor of the thirteen year old Duke of Bordeaux Henri d'Artois (1820 – 1883), the exiled Crown Prince and grandson of Charles X. As a professor of the École Polytechnique, Cauchy had been a notoriously bad lecturer, assuming levels of understanding that only a few of his best students could reach, and cramming his allotted time with too much material. The young Duke had neither taste nor talent for either mathematics or science, so student and teacher were a perfect mismatch. Although Cauchy took his mission very seriously, he did this with great clumsiness, and with surprising lack of authority over the Duke.

During his civil engineering days, Cauchy once had been briefly in charge of repairing a few of the Parisian sewers, and he made the mistake of telling his pupil this; with great malice, the young Duke went about saying that Mister Cauchy started his career in the sewers of Paris. His role as tutor lasted until the Duke became eighteen years old, in September 1838. Cauchy did hardly any research during those five years, while the Duke acquired a life long dislike of mathematics. The only good that came out of this episode was Cauchy's promotion to Baron, a title that Cauchy set great store by. In 1834, his wife and two daughters moved to Prague, and Cauchy was finally reunited with his family, after four years of exile.

Cauchy returned to Paris and his position at the Academy of Sciences late in 1838. He could not regain his teaching positions, because he still refused to swear an oath of allegiance. However, he desperately wanted to regain a formal position in Parisian science.

In August 1839 a vacancy appeared in the Bureau des Longitudes. This Bureau had some resemblance to the Academy; for instance, it had the right to co-opt its members. Further, it was believed that members of the Bureau could "forget" about the oath of allegiance, although formally, unlike the Academicians, they were obliged to take it. The Bureau des Longitudes was an organization founded in 1795 to solve the problem of determining position on sea - mainly the longitudinal coordinate, since latitude is easily determined from the position of the sun. Since it was thought that position on sea was best determined by astronomical observations, the Bureau had developed into an organization resembling an academy of astronomical sciences.

In November 1839 Cauchy was elected to the Bureau, and discovered immediately that the matter of the oath was not so easily dispensed with. Without his oath, the king refused to approve his election. For four years Cauchy was in the absurd position of being elected, but not being approved; hence, he was not a formal member of the Bureau, did not receive payment, could not participate in meetings, and could not submit papers. Still Cauchy refused to take any oaths; however, he did feel loyal enough to direct his research to celestial mechanics. In 1840, he presented a dozen papers on this topic to the Academy. The confounded membership of the Bureau lasted until the end of 1843, when Cauchy was finally replaced by Poinsot.

All through the nineteenth century the French educational system struggled with the separation of Church and State. The Catholic Church strived for freedom of education (that is, the right to establish Catholic schools); the Church found in Cauchy a staunch and illustrious ally in this struggle. He lent his prestige and knowledge to the École Normale Écclésiastique, a school in Paris run by Jesuits, for training teachers for their colleges. He also took part in the founding of the Institut Catholique. The purpose of this institute was to counter the effects of the absence of Catholic university education in France. These activities did not make Cauchy popular with his colleagues who, on the whole, supported the Enlightenment ideals of the French Revolution. When a chair of mathematics became vacant at the Collège de France in 1843, Cauchy applied for it, but got just three out of 45 votes.

The year 1848 was the year of revolution all over Europe; revolutions broke out in numerous countries, beginning in France. King Louis - Philippe, fearful of sharing the fate of Louis XVI, fled to England. The oath of allegiance was abolished, and the road to an academic appointment was finally clear for Cauchy. On March 1, 1849, he was reinstated at the Faculté de Sciences, as a professor of mathematical astronomy. After political turmoil all through 1848, France chose to become a Republic, under the Presidency of Louis Napoleon Bonaparte, nephew of Napoleon Bonaparte, and son of Napoleon's brother, who had been installed as the first king of Holland. Soon (early 1852) the President became the Emperor of France, and took the name Napoleon III.

Not unexpectedly, the idea came up in bureaucratic circles that it would be useful to require a loyalty oath from all state functionaries, including university professors. Not always does history repeat itself, however, because this time a cabinet minister was able to convince the Emperor to exempt Cauchy from the oath. Cauchy remained a professor at the University until his death at the age of 67. He received the Last Sacraments and died at 4 a.m. during the night of May 23, 1857.

His name is one of the 72 names inscribed on the Eiffel Tower.

The genius of Cauchy was illustrated in his simple solution of the problem of Apollonius — describing a circle touching three given circles — which he discovered in 1805, his generalization of Euler's formula on polyhedra in 1811, and in several other elegant problems. More important is his memoir on wave propagation, which obtained the Grand Prix of the French Academy of Sciences in 1816. Cauchy's writings covered notable topics including: the theory of series, where he developed the notion of convergence and discovered many of the basic formulas for q-series. The theory of numbers and complex quantities; he was the first to define complex numbers as pairs of real numbers. The theory of groups and substitutions; and the theory of functions, differential equations, and determinants.

In the theory of light he worked on Fresnel's wave theory and on the dispersion and polarization of light. He also contributed significant research in mechanics, substituting the notion of the continuity of geometrical displacements for the principle of the continuity of matter. He wrote on the equilibrium of rods and elastic membranes and on waves in elastic media. He introduced a 3 × 3 symmetric matrix of numbers that is now known as the Cauchy stress tensor. In elasticity, he originated the theory of stress, and his results are nearly as valuable as those of Simeon Poisson. Other significant contributions include being the first to prove the Fermat polygonal number theorem.

Cauchy is most famous for his single handed development of complex function theory. The first pivotal theorem proved by Cauchy, now known as Cauchy's integral theorem, was the following:

where f(z) is a complex - valued function holomorphic on and within the non - self - intersecting closed curve C (contour) lying in the complex plane. The contour integral is taken along the contour C. The rudiments of this theorem can already be found in a paper that the 24 year old Cauchy presented to the Académie des Sciences (then still called "First Class of the Institute") on August 11, 1814. In full form the theorem was given in 1825. The 1825 paper is seen by many as Cauchy's most important contribution to mathematics.

In 1826 Cauchy gave a formal definition of a residue of a function. This concept regards functions that have poles — isolated singularities, i.e., points where a function goes to positive or negative infinity. If the complex - valued function f(z) can be expanded in the neighborhood of a singularity a as

where φ(z) is analytic (i.e., well - behaved without singularities), then f is said to have a pole of order n in the point a. If n = 1, the pole is called simple. The coefficient B₁ is called by Cauchy the residue of function f at a. If f is non - singular at a then the residue of f is zero at a. Clearly the residue is in the case of a simple pole equal to,

where we replaced B₁ by the modern notation of the residue.

In 1831, while in Turin, Cauchy submitted two papers to the Academy of Sciences of Turin. In the first he proposed the formula now known as Cauchy's integral formula,

where f(z) is analytic on C and within the region bounded by the contour C and the complex number a is somewhere in this region. The contour integral is taken counter - clockwise. Clearly, the integrand has a simple pole at z = a. In the second paper he presented the residue theorem,

where the sum is over all the n poles of f(z) on and within the contour C. These results of Cauchy's still form the core of complex function theory as it is taught today to physicists and electrical engineers. For quite some time, contemporaries of Cauchy ignored his theory, believing it to be too complicated. Only in the 1840s the theory started to get response, with Pierre - Alphonse Laurent being the first mathematician, besides Cauchy, making a substantial contribution (his Laurent series published in 1843).

In addition to his work on complex functions, Cauchy was the first to stress the importance of rigor in analysis. In his book Cours d'Analyse had a such an impact that Judith Grabiner writes Cauchy was "the man who taught rigorous analysis to all of Europe." This book is frequently noted as being the first place that inequalities, and δ-ε arguments were introduced into Calculus. Cauchy's arguments also included infinitesimal methods and Cauchy writes in the introduction that he has been "... unable to dispense with making the principal qualities of infinitely small quantities known...". M. Barany explains that this is because the École mandated the inclusion of infinitesimal methods against Cauchy's better judgement and the infinitesimal portions of the book were likely a late insertion. Others such as Laugwitz and Benis - Sinaceur have argued that Cauchy was not forced to teach infinitesimals, pointing out that he continued to use them in his own work as late as 1853.

In keeping with his aims of rigor Cauchy also gave an explicit definition in terms of a sequence tending to zero. Namely, such a null sequence "becomes" an infinitesimal in Cauchy's and Lazare Carnot's terminology. Sources disagree if Cauchy defined his notion of infinitesimal in terms of limits, stating the claim is ambiguous, and essentially a play on words on the term "limit". Similarly, some sources contest the claim that Cauchy introduced rigor into infinitesimals that anticipates the rigor of Weierstrass.

Barany recently argued that Cauchy possessed a kinetic notion of limit similar to Newton's. Regardless of how Cauchy viewed the rigor of using infinitesimal methods, these methods continued in practice long after Cours d'Analyse both by Cauchy and other mathematicians and can be justified by modern techniques.

He was the first to prove Taylor's theorem rigorously, establishing his well known form of the remainder. He wrote a textbook for his students at the École Polytechnique in which he developed the basic theorems of mathematical analysis as rigorously as possible. In this book he gave the necessary and sufficient condition for the existence of a limit in the form that is still taught. Also Cauchy's well known test for absolute convergence stems from this book: Cauchy condensation test. In 1829 he defined for the first time a complex function of a complex variable in another textbook. In spite of these, Cauchy's own research papers often used intuitive, not rigorous, methods; thus one of his theorems was exposed to a "counter - example" by Abel, later fixed by the introduction of the notion of uniform continuity.

In a paper published in 1855, two years before Cauchy's death, he discussed some theorems, one of which is similar to the "Argument Principle" in many modern textbooks on complex analysis. In modern control theory textbooks, the Cauchy argument principle is quite frequently used to derive the Nyquist stability criterion, which can be used to predict the stability of negative feedback amplifier and negative feedback control systems. Thus Cauchy's work has a strong impact on both pure mathematics and practical engineering.

Cauchy was very productive, in number of papers second only to Leonhard Euler. It took almost a century to collect all his writings into 27 large volumes:

• Oeuvres complètes d'Augustin Cauchy publiées sous la direction scientifique de l'Académie des sciences et sous les auspices de M. le ministre de l'Instruction publique (27 volumes) (Paris : Gauthier-Villars et fils, 1882 – 1974)

His greatest contributions to mathematical science are enveloped in the rigorous methods which he introduced; these are mainly embodied in his three great treatises:

• Cours d'analyse de l'École royale polytechnique (1821)
• Le Calcul infinitésimal (1823)
• Leçons sur les applications de calcul infinitésimal; La géométrie (1826 – 1828)

His other works include:

• Exercices d'analyse et de physique mathematique (Volume 1)
• Exercices d'analyse et de physique mathematique (Volume 2)
• Exercices d'analyse et de physique mathematique (Volume 3)
• Exercices d'analyse et de physique mathematique (Volume 4) (Paris: Bachelier, 1840 – 1847)
• Analyse algèbrique (Imprimerie Royale, 1821)
• Nouveaux exercices de mathématiques (Paris : Gauthier - Villars, 1895)
• Courses of mechanics (for the École Polytechnique)
• Higher algebra (for the Faculté des Sciences)
• Mathematical physics (for the Collège de France).

Augustin Louis Cauchy grew up in the house of a staunch royalist. This made his father flee with the family to Arcueil during the French Revolution. Their life there was apparently hard and Lois - François Cauchy spoke of living on rice, bread, and crackers during the period. A paragraph from an undated letter from Louis - François to his mother in Rouen, cited by C A Valson in La Vie et les Travaux du baron Cauchy  says:

We never had more than a half pound of bread — and sometimes not even that. This we supplement with little supply of hard crackers and rice that we are allotted. Otherwise, we are getting along quite well, which is the important thing and goes to show that human beings can get by with little. I should tell you that for my children's pap I still have a bit of fine flour, made from wheat that I grew on my own land. I had three bushels, and I also have a few pounds of potato starch. It is as white as snow and very good, too, especially for very young children. It, too, was grown on my own land.

In any event he inherited his father's staunch royalism and hence refused to take oaths to any government after the overthrow of Charles X.

He was an equally staunch Catholic and a member of the Society of Saint Vincent de Paul. He also had links to the Society of Jesus and defended them at the Academy when it was politically unwise to do so. His zeal for his faith may have led to his caring for Charles Hermite during his illness and leading Hermite to become a faithful Catholic. It also inspired Cauchy to plead on behalf of the Irish during the Potato Famine.

His royalism and religious zeal also made him contentious, which caused difficulties with his colleagues. He felt that he was mistreated for his beliefs, but his opponents felt he intentionally provoked people by berating them over religious matters or by defending the Jesuits after they had been suppressed. Niels Henrik Abel called him a "bigoted Catholic" and added he was "mad and there is nothing that can be done about him," but at the same time praised him as a mathematician. Cauchy's views were widely unpopular among mathematicians and when Guglielmo Libri Carucci dalla Sommaja was made chair in mathematics before him he, and many others, felt his views were the cause. When Libri was accused of stealing books he was replaced by Joseph Liouville which caused a rift between him and Cauchy. Another dispute concerned Jean Marie Constant Duhamel and a claim on inelastic shocks. Cauchy was later shown, by Jean - Victor Poncelet, that he was in the wrong.

Arthur Cayley F.R.S. (16 August 1821 – 26 January 1895) was a British mathematician. He helped found the modern British school of pure mathematics.

As a child, Cayley enjoyed solving complex math problems for amusement. He entered Trinity College, Cambridge, where he excelled in Greek, French, German, and Italian, as well as mathematics. He worked as a lawyer for 14 years.

He postulated the Cayley – Hamilton theorem — that every square matrix is a root of its own characteristic polynomial, and verified it for matrices of order 2 and 3. He was the first to define the concept of a group in the modern way — as a set with a binary operation satisfying certain laws. Formerly, when mathematicians spoke of "groups", they had meant permutation groups.

Arthur Cayley was born in Richmond, London, England, on 16 August 1821. His father, Henry Cayley, was a distant cousin of Sir George Cayley the aeronautics engineer innovator, and descended from an ancient Yorkshire family. He settled in Saint Petersburg, Russia, as a merchant. His mother was Maria Antonia Doughty, daughter of William Doughty. According to some writers she was Russian, but her father's name indicates an English origin. His brother was the linguist Charles Bagot Cayley. Arthur spent his first eight years in Saint Petersburg. In 1829 his parents were settled permanently at Blackheath, near London. Arthur was sent to a private school. He early showed great liking for, and aptitude in, numerical calculation. At age 14 he was sent to King's College School. The school's master observed indications of mathematical genius and advised the father to educate his son not for his own business, as he had intended, but to enter the University of Cambridge.

At the unusually early age of 17 Cayley began residence at Trinity College, Cambridge. The cause of the Analytical Society had now triumphed, and the Cambridge Mathematical Journal had been instituted by Gregory and Robert Leslie Ellis. To this journal, at the age of twenty, Cayley contributed three papers, on subjects which had been suggested by reading the Mécanique analytique of Lagrange and some of the works of Laplace.

Cayley's tutor at Cambridge was George Peacock and his private coach was William Hopkins. He finished his undergraduate course by winning the place of Senior Wrangler, and the first Smith's prize. His next step was to take the M.A. degree, and win a Fellowship by competitive examination. He continued to reside at Cambridge for four years; during which time he took some pupils, but his main work was the preparation of 28 memoirs to the Mathematical Journal.

Because of the limited tenure of his fellowship it was necessary to choose a profession; like De Morgan, Cayley chose law, and at age 25 entered at Lincoln's Inn, London. He made a specialty of conveyancing. It was while he was a pupil at the bar examination that he went to Dublin to hear Hamilton's lectures on quaternions.

His friend Sylvester, his senior by five years at Cambridge, was then an actuary, resident in London; they used to walk together round the courts of Lincoln's Inn, discussing the theory of invariants and covariants. During this period of his life, extending over fourteen years, Cayley produced between two and three hundred papers.

At Cambridge University the ancient professorship of pure mathematics is denominated the Lucasian, and is the chair which had been occupied by Isaac Newton. Around 1860, certain funds bequeathed by Lady Sadleir to the University, having become useless for their original purpose, were employed to establish another professorship of pure mathematics, called the Sadleirian. The duties of the new professor were defined to be "to explain and teach the principles of pure mathematics and to apply himself to the advancement of that science." To this chair Cayley was elected when 42 years old. He gave up a lucrative practice for a modest salary; but he never regretted the exchange, for the chair at Cambridge enabled him to end the divided allegiance between law and mathematics, and to devote his energies to the pursuit which he liked best. He at once married and settled down in Cambridge. More fortunate than Hamilton in his choice, his home life was one of great happiness. His friend and fellow investigator, Sylvester, once remarked that Cayley had been much more fortunate than himself; that they both lived as bachelors in London, but that Cayley had married and settled down to a quiet and peaceful life at Cambridge; whereas he had never married, and had been fighting the world all his days.

At first the teaching duty of the Sadleirian professorship was limited to a course of lectures extending over one of the terms of the academic year; but when the University was reformed about 1886, and part of the college funds applied to the better endowment of the University professors, the lectures were extended over two terms. For many years the attendance was small, and came almost entirely from those who had finished their career of preparation for competitive examinations; after the reform the attendance numbered about fifteen. The subject lectured on was generally that of the memoir on which the professor was for the time engaged.

The other duty of the chair — the advancement of mathematical science — was discharged in a handsome manner by the long series of memoirs which he published, ranging over every department of pure mathematics. But it was also discharged in a much less obtrusive way; he became the standing referee on the merits of mathematical papers to many societies both at home and abroad.

In 1876 he published a Treatise on Elliptic Functions, which was his only book. He took great interest in the movement for the University education of women. At Cambridge the women's colleges are Girton and Newnham. In the early days of Girton College he gave direct help in teaching, and for some years he was chairman of the council of Newnham College, in the progress of which he took the keenest interest to the last.

In 1872 he was made an honorary fellow of Trinity College, and three years later an ordinary fellow, which meant stipend as well as honor. About this time his friends subscribed for a presentation portrait. Maxwell wrote an address to the committee of subscribers who had charge of the Cayley portrait fund. The verses refer to the subjects investigated in several of Cayley's most elaborate memoirs; such as, Chapters on the Analytical Geometry of n dimensions; On the theory of Determinants; Memoir on the theory of Matrices; Memoirs on skew surfaces, otherwise Scrolls; On the delineation of a Cubic Scroll, etc.

In 1881 he received from the Johns Hopkins University, Baltimore, where Sylvester was then professor of mathematics, an invitation to deliver a course of lectures. He accepted the invitation, and lectured at Baltimore during the first five months of 1882 on the subject of the Abelian and Theta Functions.

In 1883 Cayley was President of the British Association for the Advancement of Science. The meeting was held at Southport, in the north of England. As the President's address is one of the great popular events of the meeting, and brings out an audience of general culture, it is usually made as little technical as possible. Cayley (1996) took for his subject the Progress of Pure Mathematics.

In 1889 the Cambridge University Press requested him to prepare his mathematical papers for publication in a collected form — a request which he appreciated very much. They are printed in magnificent quarto volumes, of which seven appeared under his own editorship. While editing these volumes, he was suffering from a painful internal malady, to which he succumbed on 26 January 1895, in the 74th year of his age. When the funeral took place, a great assemblage met in Trinity Chapel, comprising members of the University, official representatives of Russia and America, and many of the most illustrious philosophers of Britain.

The remainder of his papers were edited by Prof. Forsyth, his successor in the Sadleirian Chair. The Collected Mathematical papers number thirteen quarto volumes, and contain 967 papers. Cayley retained to the last his fondness for novel - reading and for traveling. He also took special pleasure in paintings and architecture, and he practiced water color painting, which he found useful sometimes in making mathematical diagrams.