• Mathematician and Physicist Jules Henri Poincaré, 1854
• Mathematician Charles Émile Picard, 1856

Poincaré made clear importance of paying attention to the invariance of laws of physics under different transformations, and was the first to present the Lorentz transformations in their modern symmetrical form. Poincaré discovered the remaining relativistic velocity transformations and recorded them in a letter to Dutch physicist Hendrik Lorentz (1853 – 1928) in 1905. Thus, he obtained perfect invariance of all of Maxwell's equations, an important step in the formulation of the theory of special relativity.

The Poincaré group used in physics and mathematics was named after him.

Poincaré was born on 29 April 1854 in Cité Ducale neighborhood, Nancy, Meurthe - et - Moselle into an influential family. His father Leon Poincaré (1828 – 1892) was a professor of medicine at the University of Nancy. His adored younger sister Aline married the spiritual philosopher Emile Boutroux. Another notable member of Jules' family was his cousin, Raymond Poincaré, who would become the President of France, 1913 to 1920, and a fellow member of the Académie française.

During his childhood he was seriously ill for a time with diphtheria and received special instruction from his mother, Eugénie Launois (1830 – 1897).

In 1862, Henri entered the Lycée in Nancy (now renamed the Lycée Henri Poincaré in his honor, along with the University of Nancy). He spent eleven years at the Lycée and during this time he proved to be one of the top students in every topic he studied. He excelled in written composition. His mathematics teacher described him as a "monster of mathematics" and he won first prizes in the concours général, a competition between the top pupils from all the Lycées across France. His poorest subjects were music and physical education, where he was described as "average at best". However, poor eyesight and a tendency towards absentmindedness may explain these difficulties. He graduated from the Lycée in 1871 with a Bachelor's degree in letters and sciences.

During the Franco - Prussian War of 1870 he served alongside his father in the Ambulance Corps.

Poincaré entered the École Polytechnique in 1873. There he studied mathematics as a student of Charles Hermite, continuing to excel and publishing his first paper (Démonstration nouvelle des propriétés de l'indicatrice d'une surface) in 1874. He graduated in 1875 or 1876. He went on to study at the École des Mines, continuing to study mathematics in addition to the mining engineering syllabus and received the degree of ordinary engineer in March 1879.

As a graduate of the École des Mines he joined the Corps des Mines as an inspector for the Vesoul region in northeast France. He was on the scene of a mining disaster at Magny in August 1879 in which 18 miners died. He carried out the official investigation into the accident in a characteristically thorough and humane way.

At the same time, Poincaré was preparing for his doctorate in sciences in mathematics under the supervision of Charles Hermite. His doctoral thesis was in the field of differential equations. It was named Sur les propriétés des fonctions définies par les équations différences. Poincaré devised a new way of studying the properties of these equations. He not only faced the question of determining the integral of such equations, but also was the first person to study their general geometric properties. He realized that they could be used to model the behavior of multiple bodies in free motion within the solar system. Poincaré graduated from the University of Paris in 1879.

Soon after, he was offered a post as junior lecturer in mathematics at Caen University, but he never fully abandoned his mining career to mathematics. He worked at the Ministry of Public Services as an engineer in charge of northern railway development from 1881 to 1885. He eventually became chief engineer of the Corps de Mines in 1893 and inspector general in 1910.

Beginning in 1881 and for the rest of his career, he taught at the University of Paris (the Sorbonne). He was initially appointed as the maître de conférences d'analyse (associate professor of analysis). Eventually, he held the chairs of Physical and Experimental Mechanics, Mathematical Physics and Theory of Probability, and Celestial Mechanics and Astronomy.

Also in that same year, Poincaré married Miss Poulain d'Andecy. Together they had four children: Jeanne (born 1887), Yvonne (born 1889), Henriette (born 1891), and Léon (born 1893).

In 1887, at the young age of 32, Poincaré was elected to the French Academy of Sciences. He became its president in 1906, and was elected to the Académie française in 1909.

In 1887 he won Oscar II, King of Sweden's mathematical competition for a resolution of the three - body problem concerning the free motion of multiple orbiting bodies.

In 1893, Poincaré joined the French Bureau des Longitudes, which engaged him in the synchronization of time around the world. In 1897 Poincaré backed an unsuccessful proposal for the decimalization of circular measure, and hence time and longitude. It was this post which led him to consider the question of establishing international time zones and the synchronization of time between bodies in relative motion.

In 1899, and again more successfully in 1904, he intervened in the trials of Alfred Dreyfus. He attacked the spurious scientific claims of some of the evidence brought against Dreyfus, who was a Jewish officer in the French army charged with treason by fellow colleagues.

In 1912, Poincaré underwent surgery for a prostate problem and subsequently died from an embolism on 17 July 1912, in Paris. He was 58 years of age. He is buried in the Poincaré family vault in the Cemetery of Montparnasse, Paris.

A former French Minister of Education, Claude Allègre, has recently proposed that Poincaré be reburied in the Panthéon in Paris, which is reserved for French citizens only of the highest honor.

Poincaré had two notable doctoral students at the University of Paris, Louis Bachelier (1900) and Dimitrie Pompeiu (1905).

Poincaré made many contributions to different fields of pure and applied mathematics such as: celestial mechanics, fluid mechanics, optics, electricity, telegraphy, capillarity, elasticity, thermodynamics, potential theory, quantum theory, theory of relativity and physical cosmology.

He was also a popularizer of mathematics and physics and wrote several books for the lay public.

Among the specific topics he contributed to are the following:

• algebraic topology
• the theory of analytic functions of several complex variables
• the theory of abelian functions
• algebraic geometry
• Poincaré was responsible for formulating one of the most famous problems in mathematics, the Poincaré conjecture, proven in 2003 by Grigori Perelman.
• Poincaré recurrence theorem
• hyperbolic geometry
• number theory
• the three-body problem
• the theory of diophantine equations
• the theory of electromagnetism
• the special theory of relativity
• In an 1894 paper, he introduced the concept of the fundamental group.
• In the field of differential equations Poincaré has given many results that are critical for the qualitative theory of differential equations, for example the Poincaré sphere and the Poincaré map.
• Poincaré on "everybody's belief" in the Normal Law of Errors (normal distribution)
• Published an influential paper providing a novel mathematical argument in support of quantum mechanics.

The problem of finding the general solution to the motion of more than two orbiting bodies in the solar system had eluded mathematicians since Newton's time. This was known originally as the three - body problem and later the n-body problem, where n is any number of more than two orbiting bodies. The n-body solution was considered very important and challenging at the close of the nineteenth century. Indeed in 1887, in honor of his 60th birthday, Oscar II, King of Sweden, advised by Gösta Mittag - Leffler, established a prize for anyone who could find the solution to the problem. The announcement was quite specific:

In case the problem could not be solved, any other important contribution to classical mechanics would then be considered to be prizeworthy. The prize was finally awarded to Poincaré, even though he did not solve the original problem. One of the judges, the distinguished Karl Weierstrass, said, "This work cannot indeed be considered as furnishing the complete solution of the question proposed, but that it is nevertheless of such importance that its publication will inaugurate a new era in the history of celestial mechanics." (The first version of his contribution even contained a serious error). The version finally printed contained many important ideas which led to the theory of chaos. The problem as stated originally was finally solved by Karl F. Sundman for n = 3 in 1912 and was generalized to the case of n > 3 bodies by Qiudong Wang in the 1990s.

Poincaré's work at the Bureau des Longitudes on establishing international time zones led him to consider how clocks at rest on the Earth, which would be moving at different speeds relative to absolute space (or the "luminiferous aether"), could be synchronized. At the same time Dutch theorist Hendrik Lorentz was developing Maxwell's theory into a theory of the motion of charged particles ("electrons" or "ions"), and their interaction with radiation. In 1895 Lorentz had introduced an auxiliary quantity (without physical interpretation) called "local time" 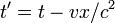and introduced the hypothesis of length contraction to explain the failure of optical and electrical experiments to detect motion relative to the aether (Michelson – Morley experiment). Poincaré was a constant interpreter (and sometimes friendly critic) of Lorentz's theory. Poincaré as a philosopher was interested in the "deeper meaning". Thus he interpreted Lorentz's theory and in so doing he came up with many insights that are now associated with special relativity. In The Measure of Time (1898), Poincaré said, " A little reflection is sufficient to understand that all these affirmations have by themselves no meaning. They can have one only as the result of a convention." He also argued that scientists have to set the constancy of the speed of light as a postulate to give physical theories the simplest form. Based on these assumptions he discussed in 1900 Lorentz's "wonderful invention" of local time and remarked that it arose when moving clocks are synchronized by exchanging light signals assumed to travel with the same speed in both directions in a moving frame.

He discussed the "principle of relative motion" in two papers in 1900 and named it the principle of relativity in 1904, according to which no physical experiment can discriminate between a state of uniform motion and a state of rest. In 1905 Poincaré wrote to Lorentz about Lorentz's paper of 1904, which Poincaré described as a "paper of supreme importance." In this letter he pointed out an error Lorentz had made when he had applied his transformation to one of Maxwell's equations, that for charge - occupied space, and also questioned the time dilation factor given by Lorentz. In a second letter to Lorentz, Poincaré gave his own reason why Lorentz's time dilation factor was indeed correct after all: it was necessary to make the Lorentz transformation form a group and gave what is now known as the relativistic velocity - addition law. Poincaré later delivered a paper at the meeting of the Academy of Sciences in Paris on 5 June 1905 in which these issues were addressed. In the published version of that he wrote:

and showed that the arbitrary function 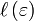must be unity for all (Lorentz had set 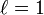by a different argument) to make the transformations form a group. In an enlarged version of the paper that appeared in 1906 Poincaré pointed out that the combination 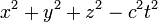is invariant. He noted that a Lorentz transformation is merely a rotation in four - dimensional space about the origin by introducing 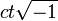as a fourth imaginary coordinate, and he used an early form of four - vectors. Poincaré expressed a disinterest in a four - dimensional reformulation of his new mechanics in 1907, because in his opinion the translation of physics into the language of four - dimensional geometry would entail too much effort for limited profit. So it was Hermann Minkowski who worked out the consequences of this notion in 1907.

Like others before, Poincaré (1900) discovered a relation between mass and electromagnetic energy. While studying the conflict between the action / reaction principle and Lorentz ether theory, he tried to determine whether the center of gravity still moves with a uniform velocity when electromagnetic fields are included. He noticed that the action / reaction principle does not hold for matter alone, but that the electromagnetic field has its own momentum. Poincaré concluded that the electromagnetic field energy of an electromagnetic wave behaves like a fictitious fluid ("fluide fictif") with a mass density of E/c². If the center of mass frame is defined by both the mass of matter and the mass of the fictitious fluid, and if the fictitious fluid is indestructible — it's neither created or destroyed — then the motion of the center of mass frame remains uniform. But electromagnetic energy can be converted into other forms of energy. So Poincaré assumed that there exists a non - electric energy fluid at each point of space, into which electromagnetic energy can be transformed and which also carries a mass proportional to the energy. In this way, the motion of the center of mass remains uniform. Poincaré said that one should not be too surprised by these assumptions, since they are only mathematical fictions.

However, Poincaré's resolution led to a paradox when changing frames: if a Hertzian oscillator radiates in a certain direction, it will suffer a recoil from the inertia of the fictitious fluid. Poincaré performed a Lorentz boost (to order v/c) to the frame of the moving source. He noted that energy conservation holds in both frames, but that the law of conservation of momentum is violated. This would allow perpetual motion, a notion which he abhorred. The laws of nature would have to be different in the frames of reference, and the relativity principle would not hold. Therefore he argued that also in this case there has to be another compensating mechanism in the ether.

Poincaré himself came back to this topic in his St. Louis lecture (1904). This time (and later also in 1908) he rejected the possibility that energy carries mass and criticized the ether solution to compensate the above mentioned problems:

The apparatus will recoil as if it were a cannon and the projected energy a ball, and that contradicts the principle of Newton, since our present projectile has no mass; it is not matter, it is energy. [..] Shall we say that the space which separates the oscillator from the receiver and which the disturbance must traverse in passing from one to the other, is not empty, but is filled not only with ether, but with air, or even in inter - planetary space with some subtile, yet ponderable fluid; that this matter receives the shock, as does the receiver, at the moment the energy reaches it, and recoils, when the disturbance leaves it? That would save Newton's principle, but it is not true. If the energy during its propagation remained always attached to some material substratum, this matter would carry the light along with it and Fizeau has shown, at least for the air, that there is nothing of the kind. Michelson and Morley have since confirmed this. We might also suppose that the motions of matter proper were exactly compensated by those of the ether; but that would lead us to the same considerations as those made a moment ago. The principle, if thus interpreted, could explain anything, since whatever the visible motions we could imagine hypothetical motions to compensate them. But if it can explain anything, it will allow us to foretell nothing; it will not allow us to choose between the various possible hypotheses, since it explains everything in advance. It therefore becomes useless.

He also discussed two other unexplained effects: (1) non - conservation of mass implied by Lorentz's variable mass γm, Abraham's theory of variable mass and Kaufmann's experiments on the mass of fast moving electrons and (2) the non - conservation of energy in the radium experiments of Madame Curie.

It was Albert Einstein's concept of mass – energy equivalence (1905) that a body losing energy as radiation or heat was losing mass of amount m = E/c² that resolved Poincaré's paradox, without using any compensating mechanism within the ether. The Hertzian oscillator loses mass in the emission process, and momentum is conserved in any frame. However, concerning Poincaré's solution of the Center of Gravity problem, Einstein noted that Poincaré's formulation and his own from 1906 were mathematically equivalent.

Einstein's first paper on relativity was published three months after Poincaré's short paper, but before Poincaré's longer version. It relied on the principle of relativity to derive the Lorentz transformations and used a similar clock synchronization procedure (Einstein synchronisation) that Poincaré (1900) had described, but was remarkable in that it contained no references at all. Poincaré never acknowledged Einstein's work on special relativity. Einstein acknowledged Poincaré in the text of a lecture in 1921 called Geometrie und Erfahrung in connection with non - Euclidean geometry, but not in connection with special relativity. A few years before his death Einstein commented on Poincaré as being one of the pioneers of relativity, saying "Lorentz had already recognized that the transformation named after him is essential for the analysis of Maxwell's equations, and Poincaré deepened this insight still further ...."

Poincaré's work in the development of special relativity is well recognized, though most historians stress that despite many similarities with Einstein's work, the two had very different research agendas and interpretations of the work. Poincaré developed a similar physical interpretation of local time and noticed the connection to signal velocity, but contrary to Einstein he continued to use the ether - concept in his papers and argued that clocks in the ether show the "true" time, and moving clocks show the local time. So Poincaré tried to keep the relativity principle in accordance with classical concepts, while Einstein developed a mathematically equivalent kinematics based on the new physical concepts of the relativity of space and time. While this is the view of most historians, a minority go much further, such as E.T. Whittaker, who held that Poincaré and Lorentz were the true discoverers of Relativity.

Poincaré's work habits have been compared to a bee flying from flower to flower. Poincaré was interested in the way his mind worked; he studied his habits and gave a talk about his observations in 1908 at the Institute of General Psychology in Paris. He linked his way of thinking to how he made several discoveries.

The mathematician Darboux claimed he was un intuitif (intuitive), arguing that this is demonstrated by the fact that he worked so often by visual representation. He did not care about being rigorous and disliked logic. He believed that logic was not a way to invent but a way to structure ideas and that logic limits ideas.

Poincaré's mental organization was not only interesting to Poincaré himself but also to Toulouse, a psychologist of the Psychology Laboratory of the School of Higher Studies in Paris. Toulouse wrote a book entitled Henri Poincaré (1910). In it, he discussed Poincaré's regular schedule:

• He worked during the same times each day in short periods of time. He undertook mathematical research for four hours a day, between 10 a.m. and noon then again from 5 p.m. to 7 p.m.. He would read articles in journals later in the evening.

• His normal work habit was to solve a problem completely in his head, then commit the completed problem to paper.

• He was ambidextrous and nearsighted.

• His ability to visualize what he heard proved particularly useful when he attended lectures, since his eyesight was so poor that he could not see properly what the lecturer wrote on the blackboard.

These abilities were offset to some extent by his shortcomings:

• He was physically clumsy and artistically inept.

• He was always in a rush and disliked going back for changes or corrections.

• He never spent a long time on a problem since he believed that the subconscious would continue working on the problem while he consciously worked on another problem.

In addition, Toulouse stated that most mathematicians worked from principles already established while Poincaré started from basic principles each time.

His method of thinking is well summarized as:

Habitué à négliger les détails et à ne regarder que les cimes, il passait de l'une à l'autre avec une promptitude surprenante et les faits qu'il découvrait se groupant d'eux - mêmes autour de leur centre étaient instantanément et automatiquement classés dans sa mémoire. (Accustomed to neglecting details and to looking only at mountain tops, he went from one peak to another with surprising rapidity, and the facts he discovered, clustering around their center, were instantly and automatically pigeonholed in his memory.)

—Belliver (1956)

Poincaré had philosophical views opposite to those of Bertrand Russell and Gottlob Frege, who believed that mathematics was a branch of logic. Poincaré strongly disagreed, claiming that intuition was the life of mathematics. Poincaré gives an interesting point of view in his book Science and Hypothesis:

For a superficial observer, scientific truth is beyond the possibility of doubt; the logic of science is infallible, and if the scientists are sometimes mistaken, this is only from their mistaking its rule.

Poincaré believed that arithmetic is a synthetic science. He argued that Peano's axioms cannot be proven non - circularly with the principle of induction, therefore concluding that arithmetic is a priori synthetic and not analytic. Poincaré then went on to say that mathematics cannot be deduced from logic since it is not analytic. His views were similar to those of Immanuel Kant. He strongly opposed Cantorian set theory, objecting to its use of impredicative definitions.

However, Poincaré did not share Kantian views in all branches of philosophy and mathematics. For example, in geometry, Poincaré believed that the structure of non - Euclidean space can be known analytically. Poincaré held that convention plays an important role in physics. His view (and some later, more extreme versions of it) came to be known as "conventionalism". Poincaré believed that Newton's first law was not empirical but is a conventional framework assumption for mechanics. He also believed that the geometry of physical space is conventional. He considered examples in which either the geometry of the physical fields or gradients of temperature can be changed, either describing a space as non - Euclidean measured by rigid rulers, or as a Euclidean space where the rulers are expanded or shrunk by a variable heat distribution. However, Poincaré thought that we were so accustomed to Euclidean geometry that we would prefer to change the physical laws to save Euclidean geometry rather than shift to a non - Euclidean physical geometry.

Poincaré's famous lectures before the Société de Psychologie in Paris (published as Science and Hypothesis, The Value of Science, and Science and Method) were cited by Jacques Hadamard as the source for the idea that creativity and invention consist of two mental stages, first random combinations of possible solutions to a problem, followed by a critical evaluation.

Although he most often spoke of a deterministic universe, Poincaré said that the subconscious generation of new possibilities involves chance.

It is certain that the combinations which present themselves to the mind in a kind of sudden illumination after a somewhat prolonged period of unconscious work are generally useful and fruitful combinations... all the combinations are formed as a result of the automatic action of the subliminal ego, but those only which are interesting find their way into the field of consciousness... A few only are harmonious, and consequently at once useful and beautiful, and they will be capable of affecting the geometrician's special sensibility I have been speaking of; which, once aroused, will direct our attention upon them, and will thus give them the opportunity of becoming conscious... In the subliminal ego, on the contrary, there reigns what I would call liberty, if one could give this name to the mere absence of discipline and to disorder born of chance.

Poincaré's two stages — random combinations followed by selection — became the basis for Daniel Dennett's two - stage model of free will.

Charles Émile Picard FRS (24 July 1856 – 11 December 1941) was a French mathematician. He was elected the fifteenth member to occupy seat 1 of the Académie Française in 1924.

Picard's mathematical papers, textbooks, and many popular writings exhibit an extraordinary range of interests, as well as an impressive mastery of the mathematics of his time. Modern students of complex variables are probably familiar with two of his named theorems. His lesser theorem states that every non constant entire function takes every value in the complex plane, with perhaps one exception. His greater theorem states that an analytic function with an essential singularity takes every value infinitely often, with perhaps one exception, in any neighborhood of the singularity. He also made important contributions in the theory of differential equations, including work on Picard – Vessiot theory, Painlevé transcendents and his introduction of a kind of symmetry group for a linear differential equation, the Picard group. In connection with his work on function theory, he was one of the first mathematicians to use the emerging ideas of algebraic topology. In addition to his path breaking theoretical work, Picard also made important contributions to applied mathematics, including the theories of telegraphy and elasticity. His collected papers run to four volumes.

Like his contemporary, Henri Poincaré, Picard was much concerned with the training of mathematics, physics, and engineering students. He wrote a classic textbook on analysis and one of the first textbooks on the theory of relativity. Picard's popular writings include biographies of many leading French mathematicians, including his father in law, Charles Hermite.