<Back to Index>
- Physicist Max Born, 1882
- Physicist Paul Adrien Maurice Dirac, 1902
PAGE SPONSOR
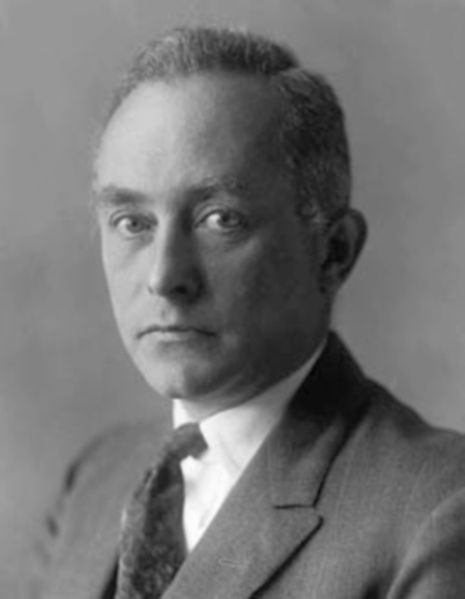
Max Born (11 December 1882 – 5 January 1970) was a German - British physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid - state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s. Born won the 1954 Nobel Prize in Physics (shared with Walther Bothe).
Max was born on December 11, 1882 in Breslau (now Wrocław, Poland), which at Born's birth was in the Prussian Province of Silesia in the German Empire. He was one of two children born to Gustav Born, (b. 22 April 1850, Kempen, d. 6 July 1900, Breslau), an anatomist and embryologist, and Margarethe ('Gretchen') Kauffmann (b. 22 January 1856, Tannhausen, d. 29 August 1886, Breslau), from a Silesian family of industrialists.
Gustav and Gretchen married on 7 May 1881. She died when Max was just four years old, on 29 August 1886.
Max had a sister Käthe (b. 5 March 1884), and a half brother Wolfgang (b. 21 October 1892) from his father's second marriage (m. 13 September 1891) with Bertha Lipstein.
Initially educated at the König - Wilhelm - Gymnasium, Born went on to study at the University of Breslau followed by Heidelberg University and the University of Zurich. During study for his Ph.D. and Habilitation at the University of Göttingen, he came into contact with many prominent scientists and mathematicians including Klein, Hilbert, Minkowski, Runge, Schwarzschild and Voigt. In 1908 - 1909 he studied at Gonville and Caius College, Cambridge.
When Born arrived in Göttingen in 1904, Klein, Hilbert and Minkowski were the high priests of mathematics and were known as the “mandarins.” Very quickly after his arrival, Born formed close ties to the latter two men. From the first class he took with Hilbert, Hilbert identified Born as having exceptional abilities and selected him as the lecture scribe, whose function was to write up the class notes for the students' mathematics reading room at the University of Göttingen. Being class scribe put Born into regular, invaluable contact with Hilbert, during which time Hilbert’s intellectual largesse benefited Born’s fertile mind. Hilbert became Born's mentor and Hilbert eventually selected him to be the first to hold the unpaid, semi - official position of Hilbert’s assistant. Born's introduction to Minkowski came through Born's stepmother, Bertha, as she knew Minkowski from dancing classes in Königsberg. The introduction netted Born invitations to the Minkowski household for Sunday dinners. In addition, while performing his duties as scribe and assistant, Born often saw Minkowski at Hilbert's house. Born’s outstanding work on elasticity – a subject near and dear to Klein – became the core of his magna cum laude Ph.D. thesis, in spite of some of Born’s irrationalities in dealing with Klein.
Born married Hedwig, née Ehrenberg, on 2 August 1913. She was
of Jewish descent on her father's side, and was a practicing Lutheran;
Born converted from Judaism to the Lutheran faith in 1914. The marriage
produced three children, including G.V.R. Born. His daughter Irene was
the mother of British born Australian
singer and actress Olivia Newton - John. Via marriage, he is related to
jurists Victor Ehrenberg (his father - in - law) and Rudolf von Jhering
(his wife's maternal grandfather), as well as Hans Ehrenberg, and is a
great uncle of British alternative comedian Ben Elton.
After Max's Habilitation in 1909, he settled in as a young academic at Göttingen as a Privatdozent (Associate Professor). In Göttingen, Born stayed at a boarding house run by Sister Annie at Dahlmannstraße 17, known as El BoKaReBo. The name was derived from the first letters of the last names of its boarders: “El” for Ella Philipson (a medical student), “Bo” for Born and Hans Bolza (a physics student), “Ka” for Theodore von Kármán (a Privatdozent), and “Re” for Albrecht Renner (a medical student). A frequent visitor to the boarding house was Paul Peter Ewald, a doctoral student of Arnold Sommerfeld on loan to David Hilbert at Göttingen as a special assistant for physics. Richard Courant, a mathematician and Privatdozent, called these people the “in group.”
From 1915 to 1919, except for a period in the German army, Born was extraordinarius professor of theoretical physics at the University of Berlin, where he formed a life long friendship with Albert Einstein. In 1919, he became ordinarius professor on the science faculty at the University of Frankfurt am Main. While there, the University of Göttingen was looking for a replacement for Peter Debye, and the Philosophy Faculty had Born at the top of their list. In negotiating for the position with the education ministry, Born arranged for another chair at Göttingen and for his long time friend and colleague James Franck to fill it. In 1921, Born became ordinarius professor of theoretical physics and Director of the new Institute of Theoretical Physics at Göttingen. While there, he formulated the now standard interpretation of the probability density function for ψ*ψ in the Schrödinger equation of quantum mechanics, published in July 1926 and for which he was awarded the Nobel Prize in Physics in 1954, some three decades later.
For the 12 years Born and Franck were at Göttingen (1921 – 1933), Born had a collaborator with shared views on basic scientific concepts — a distinct advantage for teaching and his research on the developing quantum theory. The approach of close collaboration between theoretical physicists and experimental physicists was also shared by Born at Göttingen and Arnold Sommerfeld at the University of Munich, who was ordinarius professor of theoretical physics and Director of the Institute of Theoretical Physics — also a prime mover in the development of quantum theory. Born and Sommerfeld not only shared their approach in using experimental physics to test and advance their theories, Sommerfeld, in 1922 when he was in the United States lecturing at the University of Wisconsin – Madison, sent his student Werner Heisenberg to be Born’s assistant. Heisenberg again returned to Göttingen in 1923 and completed his Habilitation under Born in 1924 and became a Privatdozent at Göttingen – the year before Heisenberg and Born published their first papers on matrix mechanics.
In 1925, Born and Werner Heisenberg formulated the matrix mechanics representation of quantum mechanics. On 9 July, Heisenberg gave Born a paper to review and submit for publication. In the paper, Heisenberg formulated quantum theory avoiding the concrete but unobservable representations of electron orbits by using parameters such as transition probabilities for quantum jumps, which necessitated using two indexes corresponding to the initial and final states. When Born read the paper, he recognized the formulation as one which could be transcribed and extended to the systematic language of matrices, which he had learned from his study under Jakob Rosanes at Breslau University. Born, with the help of his assistant and former student Pascual Jordan, began immediately to make the transcription and extension, and they submitted their results for publication; the paper was received for publication just 60 days after Heisenberg’s paper. A follow-on paper was submitted for publication before the end of the year by all three authors.
Up until this time, matrices were seldom used by physicists; they were considered to belong to the realm of pure mathematics. Gustav Mie had used them in a paper on electrodynamics in 1912 and Born had used them in his work on the lattices theory of crystals in 1921. While matrices were used in these cases, the algebra of matrices with their multiplication did not enter the picture as they did in the matrix formulation of quantum mechanics.
Born, however, had learned matrix algebra from Rosanes, as already noted, but Born had also learned Hilbert’s theory of integral equations and quadratic forms for an infinite number of variables as was apparent from a citation by Born of Hilbert’s work Grundzüge einer allgemeinen Theorie der Linearen Integralgleichungen published in 1912. Jordan, too was well equipped for the task. For a number of years, he had been an assistant to Richard Courant at Göttingen in the preparation of Courant and David Hilbert’s book Methoden der mathematischen Physik I, which was published in 1924. This book, fortuitously, contained a great many of the mathematical tools necessary for the continued development of quantum mechanics. In 1926, John von Neumann became assistant to David Hilbert, and he would coin the term Hilbert space to describe the algebra and analysis which were used in the development of quantum mechanics.
In 1928, Albert Einstein nominated Heisenberg, Born, and Jordan for the Nobel Prize in Physics, but it was not to be. The announcement of the Nobel Prize in Physics for 1932 was delayed until November 1933. It was at that time that it was announced Heisenberg had won the Prize for 1932 “for the creation of quantum mechanics, the application of which has led to the discovery of the allotropic forms of hydrogen” and Erwin Schrödinger and Paul Adrien Maurice Dirac shared the 1933 Prize "for the discovery of new productive forms of atomic theory". One can rightly ask why Born was not awarded the Prize in 1932 along with Heisenberg – Bernstein gives some speculations on this matter. One of them is related to Jordan joining the Nazi Party on 1 May 1933 and becoming a Storm Trooper. Hence, Jordan’s Party affiliations and Jordan’s links to Born may have affected Born’s chance at the Prize at that time. Bernstein also notes that when Born won the Prize in 1954, Jordan was still alive, and the Prize was awarded for the statistical interpretation of quantum mechanics, attributable alone to Born.
Heisenberg’s reaction to Born for Heisenberg himself receiving the Prize for 1932 and Born receiving the Prize in 1954 is also instructive in evaluating whether Born should have shared the Prize with Heisenberg. On 25 November 1933 Born received a letter from Heisenberg in which he said he had been delayed in writing due to a “bad conscience” that he alone had received the Prize “for work done in Göttingen in collaboration — you, Jordan and I.” Heisenberg went on to say that Born and Jordan’s contribution to quantum mechanics cannot be changed by “a wrong decision from the outside.” In 1954, Heisenberg wrote an article honoring Max Planck for his insight in 1900. In the article, Heisenberg credited Born and Jordan for the final mathematical formulation of matrix mechanics and Heisenberg went on to stress how great their contributions were to quantum mechanics, which were not “adequately acknowledged in the public eye.”
Those who received their Ph.D. degrees under Born at Göttingen included Max Delbrück, Walter Elsasser, Friedrich Hund, Pascual Jordan, Maria Goeppert - Mayer, Lothar Wolfgang Nordheim, J. Robert Oppenheimer, and Victor Weisskopf. Born’s assistants at the University of Göttingen’s Institute for Theoretical Physics included Enrico Fermi, Werner Heisenberg, Gerhard Herzberg, Friedrich Hund, Pascual Jordan, Wolfgang Pauli, Léon Rosenfeld, Edward Teller, and Eugene Wigner. Walter Heitler became an assistant to Born in 1928 and under Born completed his Habilitation in 1929. Born not only recognized talent to work with him, but he let his “superstars stretch past him.” His Ph.D. student Delbrück, and six of his assistants (Fermi, Heisenberg, Goeppert - Mayer, Herzberg, Pauli, Wigner) went on to win Nobel Prizes.
In a letter to Born in 1926, Einstein made his famous remark regarding quantum mechanics, often paraphrased as "The Old One does not play dice."
In 1933 Born emigrated from Germany. He had strong and public pacifist opinions; moreover, though Born was a Lutheran, he was classified as a Jew by the Nazi racial laws due to his ancestry, and was thus stripped of his professorship. He took up a position as Stokes Lecturer at the University of Cambridge. From 1936 to 1953 he was Tait Professor of Natural Philosophy at the University of Edinburgh, where he promoted the teaching of mathematical physics. He became a British subject and a Fellow of the Royal Society of London in 1939.
Born had a dislike for nuclear weapons research, but he still acknowledged “it might be the only way out.” Much of the theoretical power behind the development of the first atomic bomb was due to many of those surrounding him at Göttingen and working on atomic physics and quantum mechanics: three of his Ph.D. students (Maria Goeppert - Mayer, Oppenheimer and Weisskopf), three of his assistants (Fermi, Teller and Wigner), the Director of the Second Institute for Experimental Physics (James Franck), and David Hilbert’s assistant (John von Neumann).
Max and Hedwig Born retired to Bad Pyrmont (10 km south of Hamelin) in West Germany, in 1954.
Born was one of the 11 signatories to the Russell - Einstein Manifesto.
Born died in Göttingen, Germany. He is buried there in the same cemetery as Walther Nernst, Wilhelm Weber, Max von Laue, Max Planck, and David Hilbert.
In memory of his important contributions, the Max Born prize was created by the German Physical Society and the British Institute of Physics. It is awarded annually.
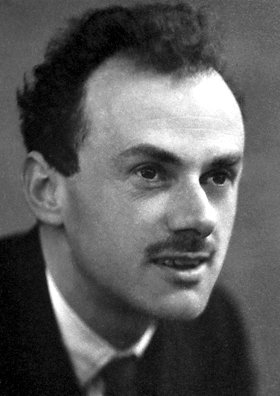
Paul Adrien Maurice Dirac, OM, FRS (8 August 1902 – 20 October 1984) was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics. He held the Lucasian Chair of Mathematics at the University of Cambridge, was a member of the Center for Theoretical Studies, University of Miami, and spent the last decade of his life at Florida State University.
Among other discoveries, he formulated the Dirac equation, which describes the behavior of fermions, and predicted the existence of antimatter.
Dirac shared the Nobel Prize in Physics for 1933 with Erwin
Schrödinger, "for the discovery of new productive forms of atomic
theory."
Paul Adrien Maurice Dirac was born at his parents' home in Bristol, England, on 8 August 1902, and grew up in the Bishopston area of the city. His father, Charles Adrien Ladislas Dirac, was an immigrant from Saint - Maurice in the Canton of Valais, Switzerland, who worked in Bristol as a French teacher. His mother, Florence Hannah Dirac, née Holten, the daughter of a ship's captain, was born in Cornwall, and worked as a librarian at the Bristol Central Library. Paul had a younger sister, Béatrice Isabelle Marguerite, known as Betty, and an older brother, Reginald Charles Félix, known as Felix, who committed suicide in March 1925. Dirac later recalled: "My parents were terribly distressed. I didn't know they cared so much. /.../ I never knew that parents were supposed to care for their children, but from then on I knew."
Charles and the children were officially Swiss nationals until they became naturalized on 22 October 1919. Dirac's father was strict and authoritarian, although he disapproved of corporal punishment. Dirac had a strained relationship with his father, so much so that after his death, he wrote, "I feel much freer now, and I am my own man." Charles forced his children to speak to him only in French, in order that they learn the language. When Dirac found that he could not express what he wanted to say in French, he chose to remain silent.
Dirac was educated first at Bishop Road Primary School and then at the all - boys Merchant Venturers' Technical College (later Cotham School), where his father was a French teacher. The school was an institution attached to the University of Bristol, which shared grounds and staff. It emphasized technical subjects like bricklaying, shoemaking and metal work, and modern languages. This was an unusual arrangement at a time when secondary education in Britain was still dedicated largely to the classics, and something for which Dirac would later express gratitude.
Dirac studied electrical engineering on a City of Bristol University Scholarship at the University of Bristol's engineering faculty, which was co-located with the Merchant Venturers' Technical College. Shortly before he completed his degree in 1921, he sat the entrance examination for St John's College, Cambridge. He passed, and was awarded a £70 scholarship, but this fell short of the amount of money required to live and study at Cambridge. Despite graduating with a first class honours bachelor of science degree in engineering, the economic climate of the post war depression was such that he was unable to find work as an engineer. Instead he took up an offer to study for bachelor of arts degree in mathematics at the University of Bristol free of charge. He was permitted to skip the first year of the course owing to his engineering degree.
In 1923, Dirac graduated, once again with first class honours, and
received a £140 scholarship from the Department of Scientific and
Industrial Research.
Along with his £70 scholarship from St John's College, this was enough
to live at Cambridge. There, Dirac pursued his interests in the theory
of general relativity, an interest he gained earlier as a student in
Bristol, and in the nascent field of quantum physics, under the supervision of Ralph Fowler.
Dirac noticed an analogy between the Poisson brackets of classical mechanics and the recently proposed quantization rules in Werner Heisenberg's matrix formulation of quantum mechanics. This observation allowed Dirac to obtain the quantization rules in a novel and more illuminating manner. For this work, published in 1926, he received a Ph.D. from Cambridge.
In 1928, building on 2x2 spin matrices which he discovered independently (Abraham Pais quoted Dirac as saying "I believe I got these (matrices) independently of Pauli and possibly Pauli got these independently of me") of Wolfgang Pauli's work on non - relativistic spin systems, he proposed the Dirac equation as a relativistic equation of motion for the wave function of the electron. This work led Dirac to predict the existence of the positron, the electron's antiparticle, which he interpreted in terms of what came to be called the Dirac sea. The positron was observed by Carl Anderson in 1932. Dirac's equation also contributed to explaining the origin of quantum spin as a relativistic phenomenon.
The necessity of fermions (matter being created and destroyed in Enrico Fermi's 1934 theory of beta decay), however, led to a reinterpretation of Dirac's equation as a "classical" field equation for any point particle of spin ħ/2, itself subject to quantization conditions involving anti - commutators. Thus reinterpreted, in 1934 by Werner Heisenberg, as a (quantum) field equation accurately describing all elementary matter particles - today quarks and leptons – this Dirac field equation is as central to theoretical physics as the Maxwell, Yang - Mills and Einstein field equations. Dirac is regarded as the founder of quantum electrodynamics, being the first to use that term. He also introduced the idea of vacuum polarization in the early 1930s. This work was key to the development of quantum mechanics by the next generation of theorists, and in particular Schwinger, Feynman, Sin - Itiro Tomonaga and Dyson in their formulation of quantum electrodynamics.
Dirac's Principles of Quantum Mechanics, published in 1930, is a landmark in the history of science. It quickly became one of the standard textbooks on the subject and is still used today. In that book, Dirac incorporated the previous work of Werner Heisenberg on matrix mechanics and of Erwin Schrödinger on wave mechanics into a single mathematical formalism that associates measurable quantities to operators acting on the Hilbert space of vectors that describe the state of a physical system. The book also introduced the delta function. Following his 1939 article, he also included the bra-ket notation in the third edition of his book, thereby contributing to its universal use nowadays.
In 1933, following his 1931 paper on magnetic monopoles, Dirac showed that the existence of a single magnetic monopole in the universe would suffice to explain the observed quantization of electrical charge. In 1975, 1982, and 2009 intriguing results suggested the possible detection of magnetic monopoles, but there is, to date, no direct evidence for their existence.
Dirac was the Lucasian Professor of Mathematics at Cambridge from 1932 to 1969. In 1937, he proposed a speculative cosmological model based on the so-called large numbers hypothesis. During World War II, he conducted important theoretical and experimental research on uranium enrichment by gas centrifuge.
Dirac's quantum electrodynamics made predictions that were – more often than not – infinite and therefore unacceptable. A workaround known as renormalization was developed, but Dirac never accepted this. "I must say that I am very dissatisfied with the situation," he said in 1975, "because this so-called 'good theory' does involve neglecting infinities which appear in its equations, neglecting them in an arbitrary way. This is just not sensible mathematics. Sensible mathematics involves neglecting a quantity when it is small – not neglecting it just because it is infinitely great and you do not want it!" His refusal to accept renormalization resulted in his work on the subject moving increasingly out of the mainstream. However, from his once rejected notes he managed to work on putting quantum electrodynamics on "logical foundations" based on Hamiltonian formalism that he formulated. He found a rather novel way of deriving the anomalous magnetic moment "Schwinger term" and also the Lamb shift, afresh, using the Heisenberg picture and without using the joining method used by Weisskopf and French, the two pioneers of modern QED, Schwinger and Feynman, in 1963. That was two years before the Tomonaga - Schwinger - Feynman QED was given formal recognition by an award of the Nobel Prize for physics. Weisskopf and French (FW) were the first to obtain the correct result for the Lamb shift and the anomalous magnetic moment of the electron. At first FW results did not agree with the incorrect but independent results of Feynman and Schwinger (Schweber SS 1994 "QED and the men who made it: Dyson, Feynman, Schwinger and Tomonaga", Princeton: PUP). The 1963 – 1964 lectures Dirac gave on quantum field theory at Yeshiva University were published in 1966 as the Belfer Graduate School of Science, Monograph Series Number, 3. After having relocated to Florida in order to be near his elder daughter, Mary, Dirac spent his last fourteen years (of both life and physics research) at the University of Miami in Coral Gables, Florida, and Florida State University in Tallahassee, Florida.
In the 1950s in his search for a better QED, Paul Dirac developed the Hamiltonian theory of constraints (Canad J Math 1950 vol 2, 129; 1951 vol 3, 1) based on lectures that he delivered at the 1949 International Mathematical Congress in Canada. Dirac (1951 “The Hamiltonian Form of Field Dynamics” Canad Jour Math, vol 3 ,1) had also solved the problem of putting the Tomonaga - Schwinger equation into the Schrödinger representation (See Phillips R J N 1987 “Tributes to Dirac” p31 London: Adam Hilger) and given explicit expressions for the scalar meson field (spin zero pion or pseudoscalar meson), the vector meson field (spin one rho meson), and the electromagnetic field (spin one massless boson, photon).
The Hamiltonian of constrained systems is one of Dirac’s many
masterpieces. It is a powerful generalization of Hamiltonian theory that
remains valid for curved spacetime. The equations for the Hamiltonian
involve only six degrees of freedom described by 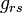 ,
,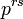 for each point of the surface on which the state is considered. The
for each point of the surface on which the state is considered. The 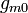 (m = 0,1,2,3) appear in the theory only through the variables
(m = 0,1,2,3) appear in the theory only through the variables 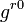 ,
, 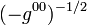 which occur as arbitrary coefficients in the equations of motion. H=∫
which occur as arbitrary coefficients in the equations of motion. H=∫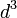 x[
x[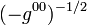
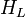 –
– 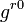 /
/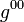
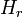 ] There are four constraints or weak equations for each point of the surface
] There are four constraints or weak equations for each point of the surface 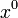 = constant. Three of them
= constant. Three of them 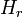 form the four vector density in the surface. The fourth
form the four vector density in the surface. The fourth 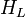 is a 3-dimensional scalar density in the surface
is a 3-dimensional scalar density in the surface 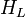 ≈0;
≈0; 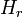 ≈0 (r = 1, 2, 3)
≈0 (r = 1, 2, 3)
In the late 1950s he applied the Hamiltonian methods he had developed to cast Einstein’s general relativity in Hamiltonian form (Proc Roy Soc 1958, A vol 246, 333, Phys Rev 1959,vol 114, 924) and to bring to a technical completion the quantization problem of gravitation and bring it also closer to the rest of physics according to Salam and DeWitt. In 1959 also he gave an invited talk on "Energy of the Gravitational Field" at the New York Meeting of the American Physical Society later published in 1959 Phys Rev Lett 2, 368. In 1964 he published his “Lectures on Quantum Mechanics” (London: Academic) which deals with constrained dynamics of nonlinear dynamical systems including quantization of curved spacetime. He also published a paper entitled “Quantization of the Gravitational Field” in 1967 ICTP / IAEA Trieste Symposium on Contemporary Physics.
If one considers waves moving in the direction 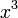 resolved into the corresponding Fourier components (r, s = 1, 2, 3), the
variables in the degrees of freedom 13, 23, 33 are affected by the changes
in the coordinate system whereas those in the degrees of freedom 12,
(11 - 22) remain invariant under such changes. The expression for the
energy splits up into terms each associated with one of these six
degrees of freedom without any cross terms associated with two of them.
The degrees of freedom 13, 23, 33 do not appear at all in the expression
for energy of gravitational waves in the direction
resolved into the corresponding Fourier components (r, s = 1, 2, 3), the
variables in the degrees of freedom 13, 23, 33 are affected by the changes
in the coordinate system whereas those in the degrees of freedom 12,
(11 - 22) remain invariant under such changes. The expression for the
energy splits up into terms each associated with one of these six
degrees of freedom without any cross terms associated with two of them.
The degrees of freedom 13, 23, 33 do not appear at all in the expression
for energy of gravitational waves in the direction 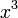 .
The two degrees of freedom 12, (11 - 22) contribute a positive definite
amount of such a form to represent the energy of gravitational waves.
These two degrees of freedom correspond in the language of quantum
theory, to the gravitational photons (gravitons)
with spin +2 or -2 in their direction of motion. The degrees of freedom
(11 + 22) gives rise to the Newtonian potential energy term showing the
gravitational force between the two positive mass is attractive and the
self energy of every mass is negative.
.
The two degrees of freedom 12, (11 - 22) contribute a positive definite
amount of such a form to represent the energy of gravitational waves.
These two degrees of freedom correspond in the language of quantum
theory, to the gravitational photons (gravitons)
with spin +2 or -2 in their direction of motion. The degrees of freedom
(11 + 22) gives rise to the Newtonian potential energy term showing the
gravitational force between the two positive mass is attractive and the
self energy of every mass is negative.
Amongst his many students was John Polkinghorne,
who recalls that Dirac "was once asked what was his fundamental belief.
He strode to a blackboard and wrote that the laws of nature should be
expressed in beautiful equations."
Dirac married Eugene Wigner's sister, Margit, in 1937. He adopted Margit's two children, Judith and Gabriel. Paul and Margit Dirac had two children together, both daughters, Mary Elizabeth and Florence Monica.
Margit, known as Manci, visited her brother in 1934 in Princeton, New Jersey, from her native Hungary and, while at dinner at the Annex Restaurant (1930s – 2006), met the "lonely looking man at the next table." This account came from a physicist from Korea who met and was influenced by Dirac, Y.S. Kim, who has also written: "It is quite fortunate for the physics community that Manci took good care of our respected Paul A.M. Dirac. Dirac published eleven papers during the period 1939 – 46.... Dirac was able to maintain his normal research productivity only because Manci was in charge of everything else."
A reviewer of the 2009 biography writes: "Dirac blamed his
[emotional] frailties on his father, a Swiss immigrant who bullied his
wife, chivvied his children and insisted Paul spoke only French at home,
even though the Diracs lived in Bristol. 'I never knew love or
affection when I was a child,' Dirac once said." She also writes that
"[t]he problem lay with his genes. Both father and son had autism,
to differing degrees. Hence the Nobel winner's reticence,
literal - mindedness, rigid patterns of behavior and self - centerdness.
[Quoting the biography:] 'Dirac's traits as a person with autism were
crucial to his success as a theoretical physicist: his ability to order
information about mathematics and physics in a systematic way, his
visual imagination, his self - centerdness, his concentration and
determination.'"
Dirac was known among his colleagues for his precise and taciturn nature. His colleagues in Cambridge jokingly defined a unit of a dirac which was one word per hour. When Niels Bohr complained that he did not know how to finish a sentence in a scientific article he was writing, Dirac replied, "I was taught at school never to start a sentence without knowing the end of it." He criticized the physicist J. Robert Oppenheimer's interest in poetry: "The aim of science is to make difficult things understandable in a simpler way; the aim of poetry is to state simple things in an incomprehensible way. The two are incompatible."
Dirac himself wrote in his diary during his postgraduate years that he concentrated solely on his research, and only stopped on Sunday, when he took long strolls alone.
An anecdote recounted in a review of the 2009 biography tells of Werner Heisenberg and Dirac sailing on a cruise ship to a conference in Japan in August 1929. "Both still in their twenties, and unmarried, they made an odd couple. Heisenberg was a ladies' man who constantly flirted and danced, while Dirac — 'an Edwardian geek', as [biographer] Graham Farmelo puts it — suffered agonies if forced into any kind of socializing or small talk. 'Why do you dance?' Dirac asked his companion. 'When there are nice girls, it is a pleasure,' Heisenberg replied. Dirac pondered this notion, then blurted out: 'But, Heisenberg, how do you know beforehand that the girls are nice?'"
According to a story told in different versions, a friend or student visited Dirac, not knowing of his marriage. Noticing the visitor's surprise at seeing an attractive woman in the house, Dirac said, "This is... this is Wigner's sister". Margit Dirac told both George Gamow and Anton Capri in the 1960s that her husband had actually said, "Allow me to present Wigner's sister, who is now my wife."
Another story told of Dirac is that when he first met the young Richard Feynman at a conference, he said after a long silence "I have an equation. Do you have one too?".
Dirac was also noted for his personal modesty. He called the equation for the time evolution
of a quantum mechanical operator, which he was the first to write down,
the "Heisenberg equation of motion". Most physicists speak of Fermi - Dirac statistics for half - integer - spin particles and Bose - Einstein statistics
for integer - spin particles. While lecturing later in life, Dirac always
insisted on calling the former "Fermi statistics". He referred to the
latter as "Einstein statistics" for reasons, he explained, of
"symmetry".
Heisenberg recollected a conversation among young participants at the 1927 Solvay Conference about Einstein and Planck's views on religion. Wolfgang Pauli, Heisenberg and Dirac took part in it. Dirac's contribution was a criticism of the political purpose of religion, which was much appreciated for its lucidity by Bohr when Heisenberg reported it to him later. Among other things, Dirac said:
| “ | I cannot understand why we idle discussing religion. If we are honest — and scientists have to be — we must admit that religion is a jumble of false assertions, with no basis in reality. The very idea of God is a product of the human imagination. It is quite understandable why primitive people, who were so much more exposed to the overpowering forces of nature than we are today, should have personified these forces in fear and trembling. But nowadays, when we understand so many natural processes, we have no need for such solutions. I can't for the life of me see how the postulate of an Almighty God helps us in any way. What I do see is that this assumption leads to such unproductive questions as why God allows so much misery and injustice, the exploitation of the poor by the rich and all the other horrors He might have prevented. If religion is still being taught, it is by no means because its ideas still convince us, but simply because some of us want to keep the lower classes quiet. Quiet people are much easier to govern than clamorous and dissatisfied ones. They are also much easier to exploit. Religion is a kind of opium that allows a nation to lull itself into wishful dreams and so forget the injustices that are being perpetrated against the people. Hence the close alliance between those two great political forces, the State and the Church. Both need the illusion that a kindly God rewards — in heaven if not on earth — all those who have not risen up against injustice, who have done their duty quietly and uncomplainingly. That is precisely why the honest assertion that God is a mere product of the human imagination is branded as the worst of all mortal sins. | ” |
Heisenberg's view was tolerant. Pauli, raised as a Catholic, had kept silent after some initial remarks, but when finally he was asked for his opinion, said: "Well, our friend Dirac has got a religion and its guiding principle is 'There is no God and Paul Dirac is His prophet.'" Everybody, including Dirac, burst into laughter.
As an author of an article appearing in the May 1963 edition of
Scientific American, his reference to God was less acerbic: "It seems to
be one of the fundamental features of nature that fundamental physical
laws are described in terms of a mathematical theory of great beauty and
power, needing quite a high standard of mathematics for one to
understand it. You may wonder: Why is nature constructed along these
lines? One can only answer that our present knowledge seems to show that
nature is so constructed. We simply have to accept it. One could
perhaps describe the situation by saying that God is a mathematician of a
very high order, and He used very advanced mathematics in constructing
the universe. Our feeble attempts at mathematics enable us to understand
a bit of the universe, and as we proceed to develop higher and higher
mathematics we can hope to understand the universe better."
In 1984, Dirac died in Tallahassee, Florida and was buried at Tallahassee's Roselawn Cemetery. Dirac's childhood home in Bristol is commemorated with a blue plaque and the nearby Dirac Road is named in recognition of his links with the city. A plaque on the wall at the Bishop Road Primary School shows the Dirac equation. A commemorative stone was erected in a garden Saint - Maurice, Switzerland, the town of origin of his father's family, on 1 August 1991. On 13 November 1995 a commemorative marker, made from Burlington green slate and inscribed with the Dirac equation, was unveiled in Westminster Abbey. Objections by the Dean of Westminster, Edward Carpenter, that Dirac was an atheist were brushed aside.
Dirac shared the 1933 Nobel Prize for physics with Erwin Schrödinger "for the discovery of new productive forms of atomic theory." Dirac was also awarded the Royal Medal in 1939 and both the Copley Medal and the Max Planck medal in 1952. He was elected a Fellow of the Royal Society in 1930, an Honorary Fellow of the American Physical Society in 1948, and an Honorary Fellow of the Institute of Physics, London, in 1971. Dirac became a member of the Order of Merit, an outstanding recognition by the land of his birth, in 1973. He had previously turned down a knighthood, as he did not want to be addressed by his first name.
In 1975, Dirac gave a series of five lectures at the University of New South Wales which were subsequently published as a book, Directions in Physics (1978). He donated the royalties from this book to the university for the establishment of the Dirac Lecture Series. The Silver Dirac Medal for the Advancement of Theoretical Physics is awarded by the University of New South Wales on the occasion of the lecture.
Immediately after his death, two organizations of professional physicists established annual awards in Dirac's memory. The Institute of Physics, the United Kingdom's professional body for physicists, awards the Paul Dirac Medal and Prize for "outstanding contributions to theoretical (including mathematical and computational) physics". The first three recipients were Stephen Hawking (1987), John Stewart Bell (1988) and Roger Penrose (1989). The Abdus Salam International Centre for Theoretical Physics (ICTP) awards the Dirac Medal of the ICTP each year on Dirac's birthday (8 August). Also, the Dirac Prize is awarded by the International Centre for Theoretical Physics in his memory. Dirac House in Bristol is the headquarters of Institute of Physics Publishing.
The Dirac - Hellmann Award at Florida State University was endowed by
Dr Bruce P. Hellmann (Dirac's last doctoral student) in 1997 to reward
outstanding work in theoretical physics by FSU researchers.
The Paul A.M. Dirac Science Library at Florida State University, which
Manci opened in December 1989, is named in his honor, and his papers
are held there. Outside is a statue of him by Gabriella Bollobás. The street on which the National High Magnetic Field Laboratory
in Tallahassee, Florida, is located was named Paul Dirac Drive. As well
as in his home town of Bristol, UK, there is also a road named after
him in Didcot Oxfordshire, Dirac Way. The BBC named its video codec Dirac in his honor.
Dirac is widely regarded as one of the world's greatest physicists. He was one of the founders of quantum mechanics and quantum electrodynamics.
His early contributions include the modern operator calculus for quantum mechanics, which he called transformation theory, and an early version of the path integral. He formulated a many - body formalism for quantum mechanics which allowed each particle to have its own proper time.
His relativistic wave equation for the electron was the first successful attack on the problem of relativistic quantum mechanics. Dirac founded quantum field theory with his reinterpretation of the Dirac equation as a many - body equation, which predicted the existence of antimatter and matter – antimatter annihilation. He was the first to formulate quantum electrodynamics, although he could not calculate arbitrary quantities because the short distance limit requires renormalization.
In an attempt to solve the quantum divergence problem, Dirac gave a classical point particle theory combining advanced and retarded waves to eliminate the classical electron self - energy. Although these classical methods did not immediately solve the problems in quantum electrodynamics, they did lead John Archibald Wheeler and Richard Feynman to formulate an alternative Green's function description for light, which eventually led to Feynman's point particle formulation of quantum field theory.
Dirac discovered the magnetic monopole solutions, the first topological configuration in physics, and used them to give the modern explanation of charge quantization. He developed constrained quantization in the 1960s, identifying the general quantum rules for arbitrary classical systems.
Dirac's quantum field analysis of the vibrations of a membrane, in the early 1960s, proved extremely useful to modern practitioners of superstring theory and its closely related successor, M-Theory.