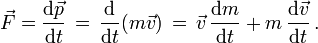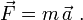• Philosopher Roger Bacon, 1214
• Physicist and Mathematician Isaac Newton, 1642

Roger Bacon was born in Ilchester in Somerset, England, possibly in 1213 or 1214 at the Ilchester Friary. The only source for his date of birth is his statement in the Opus Tertium, written in 1267, that "forty years have passed since I first learned the alphabet". The 1214 birth date assumes he was not being literal, and may have meant 40 years had passed since he matriculated at Oxford at the age of 13. If he had been literal, his birth date was more likely to have been around 1220 / 1222. In the same passage he reports that for all but two of those forty years he had always been engaged in study. His family appears to have been well off, but, during the stormy reign of Henry III of England, their property was despoiled and several members of the family were driven into exile.

Bacon studied at Oxford and may have been a disciple of Grosseteste. He became a master at Oxford, lecturing on Aristotle. There is no evidence he was ever awarded a doctorate — the title Doctor Mirabilis was posthumous and figurative. Sometime between 1237 and 1245, he began to lecture at the university of Paris, then the center of intellectual life in Europe. His whereabouts between 1247 and 1256 are uncertain, but about 1256 he became a friar in the Franciscan Order. As a Franciscan friar, Bacon no longer held a teaching post, and after 1260 his activities were further restricted by a Franciscan statute forbidding friars from publishing books or pamphlets without specific approval.

Bacon circumvented this restriction through his acquaintance with Cardinal Guy le Gros de Foulques, who became Pope Clement IV in 1265. The new Pope issued a mandate ordering Bacon to write to him concerning the place of philosophy within theology. As a result Bacon sent the Pope his Opus Majus, which presented his views on how the philosophy of Aristotle and the new science could be incorporated into a new Theology. Besides the Opus maius Bacon also sent his Opus minus, De multiplicatione specierum, and, perhaps, other works on alchemy and astrology.

Pope Clement died in 1268. Sometime between 1277 and 1279, Bacon was probably imprisoned or placed under house arrest. The circumstances for this are still mysterious. Sometime after 1278 Bacon returned to the Franciscan House at Oxford, where he continued his studies. He is believed to have died in 1294.

In the 19th century it was a widely held interpretation that Bacon was a modern experimental scientist who emerged before his time. This reflected two prevalent views of the period: an emphasis upon experiment as the principal form of scientific activity and a general acceptance of the characterization of the Middle Ages as the "Dark Ages". Some writers of the period carried this account further. For instance, according to Andrew Dickson White, Bacon was repeatedly persecuted and imprisoned because of the opposition of the medieval Church. In this view, which is still reflected in some 21st century popular science books, Bacon would be an advocate of modern experimental science who somehow emerged as an isolated figure in an age supposed to be hostile toward scientific ideas. He was also presented as a visionary; for instance Frederick Mayer wrote that Bacon predicted the invention of the submarine, automobile and airplane.

However, in the course of the 20th century, the philosophical understanding of the role of experiment in the sciences has been substantially modified. Starting with works of Pierre Duhem, Raoul Carton and Lynn Thorndike, Bacon's advocacy of scientia experimentalis has been argued to differ from modern experimental science. New historical research has also shown that medieval Christians were not generally opposed to scientific investigation and revealed the extent and variety of medieval science. In fact, many medieval sources of and influences on Bacon's scientific activity have been identified. For instance, Bacon's idea that inductively derived conclusions should be submitted for further experimental testing is very much like Robert Grosseteste's 'Method of Verification', and Bacon's work on optics and the calendar also followed the lines of inquiry of Grosseteste.

As a result, the picture of Bacon has changed. One recent study summarized that: "Bacon was not a modern, out of step with his age, or a harbinger of things to come, but a brilliant, combative, and somewhat eccentric schoolman of the thirteenth century, endeavoring to take advantage of the new learning just becoming available while remaining true to traditional notions... of the importance to be attached to philosophical knowledge". Bacon is thus seen as a leading, but not isolated figure in the beginnings of medieval universities at Paris and Oxford, among other contemporary exponents of this shift in the philosophy of science (as we call it today), including Grosseteste (who preceded Bacon), William of Auvergne, Henry of Ghent, Albert Magnus, Thomas Acquinas, John Duns Scotus, and William of Ockham.

As to the alleged persecution, the first known reference to an imprisonment originates around 80 years after Bacon's death. It says the order was given by the head of the Franciscans because of unspecified "suspected novelties". However, the fact that no earlier report has been found drives skepticism over the assertion. Moreover, current historians of science who see an incarceration as plausible typically don't connect it with Bacon's scientific writings. Instead, if it happened, scholars speculate that his troubles resulted from such things as his sympathies for radical Franciscans, attraction to contemporary prophecies, or interest in certain astrological doctrines. Bacon's personality has also been mentioned as a factor.

A recent review of the many visions that each age has held about Roger Bacon says contemporary scholarship still neglects one of the most important aspects of his life and thought: the commitment to the Franciscan order. "His Opus maius was a plea for reform addressed to the supreme spiritual head of the Christian faith, written against a background of apocalyptic expectation and informed by the driving concerns of the friars. It was designed to improve training for missionaries and to provide new skills to be employed in the defense of the Christian world against the enmity of non - Christians and of the Antichrist. It cannot usefully be read solely in the context of the history of science and philosophy."

Bacon's Opus Majus contains treatments of mathematics and optics, alchemy, and the positions and sizes of the celestial bodies.

The scientific training Bacon had received showed him the rare defects in existing academic debate. Aristotle was known only through translations, as none of the professors would learn Greek; the same was true of Scripture and many of the other auctores ("authorities") referenced in traditional education. In contrast to Aristotle's argument that facts be collected before deducing scientific truths, physical science was not carried out by observations from the natural world, but by arguments based solely on tradition and prescribed authorities (Scholasticism).

Bacon withdrew from the scholastic routine and devoted himself to languages and experimental research. The mathematicians whom he considered perfect were Peter of Maricourt and John of London, and two were good: Campanus of Novara and a Master Nicholas. Peter was the author of a famous letter to a friend, Epistola de Magnete, in which he described some of the earliest European experiments with magnetism. Campanus wrote several important works on astronomy, astrology and the calendar. Bacon often mentioned his debt to the work of Robert Grosseteste and Adam Marsh, as well as to other lesser figures. He was clearly not an isolated scholar in the thirteenth century.

In his writings, Bacon calls for a reform of theological study. Less emphasis should be placed on minor philosophical distinctions than had been the case in scholasticism. Instead, the Bible itself should return to the center of attention and theologians should thoroughly study the languages in which their original sources were composed. He was fluent in several languages and lamented the corruption of the holy texts and the works of the Greek philosophers by numerous mistranslations and misinterpretations. Furthermore, he urged all theologians to study all sciences closely, and to add them to the normal university curriculum. With regard to the obtaining of knowledge, he strongly championed experimental study over reliance on authority, arguing that "thence cometh quiet to the mind". Bacon did not restrict this approach to theological studies. He rejected the blind following of prior authorities, both in theological and scientific study, which was the accepted method of undertaking study in his day.

In the Opus Minus he criticizes his contemporaries Alexander of Hales and Albertus Magnus who, he says, had not studied the philosophy of Aristotle but only acquired their learning during their life as preachers. Albert was received at Paris as an authority equal to Aristotle, Avicenna and Averroes, leading Bacon to proclaim that "never in the world [had] such monstrosity occurred before."

The study of optics in part five of Opus Majus draws heavily on the works of both Claudius Ptolemy (his Optics in Arabic translation) and the Islamic scientists Alkindus (al-Kindi) and Alhazen (Ibn al-Haytham). He includes a discussion of the physiology of eyesight, the anatomy of the eye and the brain, and considers light, distance, position and size, direct vision, reflected vision, and refraction, mirrors and lenses. His research in optics was primarily oriented by the legacy of Alhazen through a Latin translation of the latter's monumental Kitab al-manazir (De aspectibus; Perspectivae; The Optics), while the impact of the tradition of al-Kindi (Alkindus) was principally mediated through the influence that this Muslim scholar had on the optics of Robert Grosseteste. Moreover, Bacon's investigations of the properties of the magnifying glass partly rested on the handed down legacy of Islamic opticians, mainly Alhazen, who was in his turn influenced by Ibn Sahl's 10th century legacy in dioptrics.

Drawing on the recently discovered Greco - Muslim astronomy and on the calendaric writings of Robert Grosseteste, Bacon criticized the Julian calendar, describing it as intolerable, horrible and laughable. He proposed to correct its errors by deleting a day from the calendar every 125 or 130 days.

In his own writings of 1260 – 1280 Bacon cited Secretum secretorum, which he attributed to Aristotle, far more than his contemporaries did. Often used as an argument for the special influence that this work had on Bacon's own is the manuscript of Secretum that Bacon edited, complete with his own introduction and notes, something Bacon seldom did with others' works. Although some early 20th century scholars like Robert Steele have pushed further along this path, arguing that Bacon's contact with the Secretum was a turning point in Bacon's philosophy, transforming him into an experimentalist, there is no clear reference to such a decisive impact of the Secretum in Bacon's own words. The dating of Bacon's edition of the Secretum is a key argument in this debate, but is still unresolved, with those arguing for a greater impact dating it earlier than those who urge caution in this interpretation.

The cryptic Voynich manuscript has been attributed to Bacon by various sources, including by its first recorded owner, in a book drafted by William Romaine Newbold and posthumously edited and published by Roland Grubb Kent in 1928, and in a 2005 book of Lawrence and Nancy Goldstone published by Doubleday and Broadway Books. In strongly worded terms, historians of science Lynn Thorndike and George Sarton have dismissed these claims as unsupported.

Another work of contentious date and even origin is the Epistola de Secretis Operibus Artis et Naturae, et de Nullitate Magiae (meaning Letter on the Secret Workings of Art and Nature, and on the Vanity of Magic), sometimes alternatively entitled De Mirabili Potestate Artis et Naturae (On the Wonderful Powers of Art and Nature). This treatise dismisses magical practices like necromancy, and contains most of the alchemical work attributed to Bacon, chiefly a formula for philosopher's stone, and perhaps one for gunpowder. It also contains a number of passages about hypothetical flying machines and (what we today call) submarines, attributing their first use to Alexander the Great.

Bacon is also the ascribed author of the alchemical manual Speculum Alchemiae, which was translated into English as The Mirror of Alchimy in 1597. It is a short treatise about the composition and origin of metals, espousing "conventional" (with respect to the period) Arabian theories of mercury and sulfur as the constituents of metals, and containing vague allusions to transmutation. About this work, John Maxson Stillman wrote that "there is nothing in it that is characteristic of Roger Bacon's style or ideas, nor that distinguishes it from many unimportant alchemical lucubrations of anonymous writers of the thirteenth to the sixteenth centuries". M. M. Pattison Muir had a similar opinion, and Edmund Oscar von Lippmann considered this text a pseudepigraph.

Bacon is often considered the first European to describe a mixture containing the essential ingredients of gunpowder. Based on two passages from Bacon's Opus Maius and Opus Tertium, extensively analyzed by J.R. Partington, several scholars cited by Joseph Needham concluded that Bacon had most likely witnessed at least one demonstration of Chinese firecrackers, possibly obtained with the intermediation of other Franciscans, like his friend William of Rubruck, who had visited the Mongols. The most telling passage reads: "We have an example of these things (that act on the senses) in [the sound and fire of] that children's toy which is made in many [diverse] parts of the world; i.e., a device no bigger than one's thumb. From the violence of that salt called saltpeter [together with sulphur and willow charcoal, combined into a powder] so horrible a sound is made by the bursting of a thing so small, no more than a bit of parchment [containing it], that we find [the ear assaulted by a noise] exceeding the roar of strong thunder, and a flash brighter than the most brilliant lightning."

More controversial are the claims originating with Royal Artillery colonel Henry William Lovett Hime (at the beginning of the 20th century) that a cryptogram existed in Bacon's Epistola, giving the ratio of ingredients of the mixture. These were published, among other places, in the 1911 edition of Encyclopædia Britannica. An early critic of this claim was Lynn Thorndike, starting with a letter in the 1915 edition of the journal Science , and repeated in several books of his. M.M. Pattison Muir also expressed his doubts on Hime's theory, and they were echoed by John Maxson Stillman. Robert Steele and George Sarton also joined the critics. Needham concurred with these earlier critics in their opinion that the additional passage does not originate with Bacon. In any case, the proportions claimed to have been deciphered (7:5:5 saltpeter: charcoal: sulfur) are not even useful for stuffing firecrakers, burning slowly while producing mostly smoke, and failing to ignite inside a gun barrel. The ~41% nitrate content is too low to have explosive properties.

To commemorate Bacon's seven hundredth anniversary, Professor John Erskine wrote A Pageant of the Thirteenth Century, a biographical play which was produced at Columbia University and published as a book by Columbia University Press in 1914.

An accessible description of Roger Bacon's life and times is contained in the fiction book Doctor Mirabilis, written in 1964 by the science fiction author James Blish. This is the second book in Blish's quasi - religious trilogy After Such Knowledge, and is a recounting of Bacon's life and struggle to develop a 'Universal Science'. Though thoroughly researched, with a host of references, including extensive use of Bacon's own writings, frequently in the original Latin, the book is written in the style of a novel, and Blish himself referred to it as 'fiction' or 'a vision'. Blish's view of Bacon is uncompromisingly that he was the first scientist, and he provides a postscript to the novel in which he sets forth these views. Central to his depiction of Roger Bacon is that 'He was not an inventor, an Edison or Luther Burbank, holding up a test tube with a shout of Eureka!' He was instead a theoretical scientist probing fundamental realities, and his visions of modern technology were just by-products of "...the way he normally thought — the theory of theories as tools..." Blish indicates where Bacon's writings, for example, consider Newtonian metrical frameworks for space, then reject these for something which reads remarkably like Einsteinian Relativity, and all '...breathtakingly without pause or hiccup, breezily moving without any recourse through over 800 years of physics'.

Many writers of earlier times have been attracted to Roger Bacon as the epitome of a wise and subtle possessor of forbidden knowledge, similar to Faustus. A succession of legends and unverifiable stories has grown up about him, for example, that he created a brazen talking head which could answer any question. This has a central role in the play Friar Bacon and Friar Bungay written by Robert Greene in about 1589.

Bacon also appears as first scientist in The Black Rose, the most commercially successful book by Thomas Costain, written in 1945. The Black Rose is set in the Middle Ages. Bacon's personal presence in the narrative is brief, but includes a demonstration of gunpowder and a few sentences outlining a philosophy of science which might as easily be attributed to Francis Bacon centuries later. The novel's Roger Bacon serves to motivate Costain's protagonist, a fictional Englishman who journeys to China during the reigns of Edward I and Kublai Khan. Costain's narration includes technology such as the compass, the telescope, rockets and the manufacture of paper, all described by his young adventurer with an eye toward bringing these marvels back to Bacon for analysis. Returning to England to find Bacon gone and under house arrest, the traveler begs King Edward to intercede with the pope for the Franciscan's release, arguing that with Bacon's imprisonment a great light of the world is in danger of being put out. Costain's character also comes to argue for emancipation of the Saxon villeins (serfs), linking political with intellectual enlightenment under the fictional Bacon's influence.

The Principia is generally considered to be one of the most important scientific books ever written, due, independently, to the specific physical laws the work successfully described, and for the style of the work, which assisted in setting standards for scientific publication down to the present time. Newton built the first practical reflecting telescope and developed a theory of color based on the observation that a prism decomposes white light into the many colors that form the visible spectrum. He also formulated an empirical law of cooling and studied the speed of sound. In mathematics, Newton shares the credit with Gottfried Leibniz for the development of differential and integral calculus. He also demonstrated the generalized binomial theorem, developed Newton's method for approximating the roots of a function, and contributed to the study of power series. Newton's work on infinite series was inspired by Simon Stevin's decimals. Newton was also highly religious. He was an unorthodox Christian, and wrote more on Biblical hermeneutics and occult studies than on the subjects of science and mathematics. Newton secretly rejected Trinitarianism, fearing to be accused of refusing holy orders.

Isaac Newton was born on what is retroactively considered 4 January 1643 [OS: 25 December 1642] at Woolsthorpe Manor in Woolsthorpe - by - Colsterworth, a hamlet in the county of Lincolnshire. At the time of Newton's birth, England had not adopted the Gregorian calendar and therefore his date of birth was recorded as Christmas Day, 25 December 1642. Newton was born three months after the death of his father, a prosperous farmer also named Isaac Newton. Born prematurely, he was a small child; his mother Hannah Ayscough reportedly said that he could have fit inside a quart mug (≈ 1.1 liters). When Newton was three, his mother remarried and went to live with her new husband, the Reverend Barnabus Smith, leaving her son in the care of his maternal grandmother, Margery Ayscough. The young Isaac disliked his stepfather and held some enmity towards his mother for marrying him, as revealed by this entry in a list of sins committed up to the age of 19: "Threatening my father and mother Smith to burn them and the house over them." While Newton was once engaged in his late teens to a Miss Storey, he never married, being highly engrossed in his studies and work.

From the age of about twelve until he was seventeen, Newton was educated at The King's School, Grantham (where his alleged signature can still be seen upon a library window sill). He was removed from school, and by October 1659, he was to be found at Woolsthorpe - by - Colsterworth, where his mother, widowed by now for a second time, attempted to make a farmer of him. He hated farming. Henry Stokes, master at the King's School, persuaded his mother to send him back to school so that he might complete his education. Motivated partly by a desire for revenge against a schoolyard bully, he became the top ranked student. The Cambridge psychologist Simon Baron - Cohen considers it "fairly certain" that Newton suffered from Asperger syndrome.

In June 1661, he was admitted to Trinity College, Cambridge as a sizar – a sort of work - study role. At that time, the college's teachings were based on those of Aristotle, whom Newton supplemented with modern philosophers, such as Descartes, and astronomers such as Copernicus, Galileo and Kepler. In 1665, he discovered the generalized binomial theorem and began to develop a mathematical theory that later became infinitesimal calculus. Soon after Newton had obtained his degree in August 1665, the university temporarily closed as a precaution against the Great Plague. Although he had been undistinguished as a Cambridge student, Newton's private studies at his home in Woolsthorpe over the subsequent two years saw the development of his theories on calculus, optics and the law of gravitation. In 1667, he returned to Cambridge as a fellow of Trinity. Fellows were required to become ordained priests, something Newton desired to avoid due to his unorthodox views. Luckily for Newton, there was no specific deadline for ordination and it could be postponed indefinitely. The problem became more severe later when Newton was elected for the prestigious Lucasian Chair. For such a significant appointment, ordaining normally could not be dodged. Nevertheless, Newton managed to avoid it by means of a special permission from Charles II.

Newton's work has been said "to distinctly advance every branch of mathematics then studied". His work on the subject usually referred to as fluxions or calculus, seen in a manuscript of October 1666, is now published among Newton's mathematical papers, the manuscript De analysi per aequationes numero terminorum infinitas sent by Isaac Barrow to John Collins in June 1669, Barrow identified to Collins in August of that year as:

Mr Newton, a fellow of our College, and very young ... but of an extraordinary genius and proficiency in these things.

Newton later became involved in a dispute with Leibniz over priority in the development of infinitesimal calculus. Most modern historians believe that Newton and Leibniz developed infinitesimal calculus independently, although with very different notations. Occasionally it has been suggested that Newton published almost nothing about it until 1693, and did not give a full account until 1704, while Leibniz began publishing a full account of his methods in 1684. (Leibniz's notation and "differential Method", nowadays recognized as much more convenient notations, were adopted by continental European mathematicians, and after 1820 or so, also by British mathematicians.) Such a suggestion, however, fails to notice the content of calculus which critics of Newton's time and modern times have pointed out in Book 1 of Newton's Principia itself (published 1687) and in its forerunner manuscripts, such as De motu corporum in gyrum ("On the motion of bodies in orbit"), of 1684. The Principia is not written in the language of calculus either as we know it or as Newton's (later) 'dot' notation would write it. But his work extensively uses an infinitesimal calculus in geometric form, based on limiting values of the ratios of vanishing small quantities: in the Principia itself Newton gave demonstration of this under the name of 'the method of first and last ratios' and explained why he put his expositions in this form, remarking also that 'hereby the same thing is performed as by the method of indivisibles'.

Because of this, the Principia has been called "a book dense with the theory and application of the infinitesimal calculus" in modern times and "lequel est presque tout de ce calcul" ('nearly all of it is of this calculus') in Newton's time. His use of methods involving "one or more orders of the infinitesimally small" is present in his De motu corporum in gyrum of 1684 and in his papers on motion "during the two decades preceding 1684".

Newton had been reluctant to publish his calculus because he feared controversy and criticism. He had a very close relationship with Swiss mathematician Nicolas Fatio de Duillier, who from the beginning was impressed by Newton's gravitational theory. In 1691, Duillier planned to prepare a new version of Newton's Principia, but never finished it. However, in 1693 the relationship between the two men changed. At the time, Duillier had also exchanged several letters with Leibniz.

Starting in 1699, other members of the Royal Society (of which Newton was a member) accused Leibniz of plagiarism, and the dispute broke out in full force in 1711. The Royal Society proclaimed in a study that it was Newton who was the true discoverer and labelled Leibniz a fraud. This study was cast into doubt when it was later found that Newton himself wrote the study's concluding remarks on Leibniz. Thus began the bitter controversy which marred the lives of both Newton and Leibniz until the latter's death in 1716.

Newton is generally credited with the generalized binomial theorem, valid for any exponent. He discovered Newton's identities, Newton's method, classified cubic plane curves (polynomials of degree three in two variables), made substantial contributions to the theory of finite differences, and was the first to use fractional indices and to employ coordinate geometry to derive solutions to Diophantine equations. He approximated partial sums of the harmonic series by logarithms (a precursor to Euler's summation formula), and was the first to use power series with confidence and to revert power series.

He was appointed Lucasian Professor of Mathematics in 1669 on Barrow's recommendation. In that day, any fellow of Cambridge or Oxford was required to become an ordained Anglican priest. However, the terms of the Lucasian professorship required that the holder not be active in the church (presumably so as to have more time for science). Newton argued that this should exempt him from the ordination requirement, and Charles II, whose permission was needed, accepted this argument. Thus, a conflict between Newton's religious views and Anglican orthodoxy was averted.

From 1670 to 1672, Newton lectured on optics. During this period he investigated the refraction of light, demonstrating that a prism could decompose white light into a spectrum of colors, and that a lens and a second prism could recompose the multicolored spectrum into white light.

He also showed that the colored light does not change its properties by separating out a colored beam and shining it on various objects. Newton noted that regardless of whether it was reflected or scattered or transmitted, it stayed the same color. Thus, he observed that color is the result of objects interacting with already colored light rather than objects generating the color themselves. This is known as Newton's theory of color.

From this work, he concluded that the lens of any refracting telescope would suffer from the dispersion of light into colors (chromatic aberration). As a proof of the concept, he constructed a telescope using a mirror as the objective to bypass that problem. Building the design, the first known functional reflecting telescope, today known as a Newtonian telescope, involved solving the problem of a suitable mirror material and shaping technique. Newton ground his own mirrors out of a custom composition of highly reflective speculum metal, using Newton's rings to judge the quality of the optics for his telescopes. In late 1668 he was able to produce this first reflecting telescope. In 1671, the Royal Society asked for a demonstration of his reflecting telescope. Their interest encouraged him to publish his notes On Colour, which he later expanded into his Opticks. When Robert Hooke criticized some of Newton's ideas, Newton was so offended that he withdrew from public debate. Newton and Hooke had brief exchanges in 1679 – 80, when Hooke, appointed to manage the Royal Society's correspondence, opened up a correspondence intended to elicit contributions from Newton to Royal Society transactions, which had the effect of stimulating Newton to work out a proof that the elliptical form of planetary orbits would result from a centripetal force inversely proportional to the square of the radius vector (Newton's law of universal gravitation – History and De motu corporum in gyrum). But the two men remained generally on poor terms until Hooke's death.

Newton argued that light is composed of particles or corpuscles, which were refracted by accelerating into a denser medium. He verged on soundlike waves to explain the repeated pattern of reflection and transmission by thin films (Opticks Bk.II, Props. 12), but still retained his theory of ‘fits’ that disposed corpuscles to be reflected or transmitted (Props. 13). Later physicists instead favored a purely wavelike explanation of light to account for the interference patterns, and the general phenomenon of diffraction. Today's quantum mechanics, photons and the idea of wave – particle duality bear only a minor resemblance to Newton's understanding of light.

In his Hypothesis of Light of 1675, Newton posited the existence of the ether to transmit forces between particles. The contact with the theosophist Henry More, revived his interest in alchemy. He replaced the ether with occult forces based on Hermetic ideas of attraction and repulsion between particles. John Maynard Keynes, who acquired many of Newton's writings on alchemy, stated that "Newton was not the first of the age of reason: He was the last of the magicians." Newton's interest in alchemy cannot be isolated from his contributions to science. This was at a time when there was no clear distinction between alchemy and science. Had he not relied on the occult idea of action at a distance, across a vacuum, he might not have developed his theory of gravity.

In 1704, Newton published Opticks, in which he expounded his corpuscular theory of light. He considered light to be made up of extremely subtle corpuscles, that ordinary matter was made of grosser corpuscles and speculated that through a kind of alchemical transmutation "Are not gross Bodies and Light convertible into one another, ...and may not Bodies receive much of their Activity from the Particles of Light which enter their Composition?" Newton also constructed a primitive form of a frictional electrostatic generator, using a glass globe (Optics, 8th Query).

In an article entitled "Newton, prisms, and the 'opticks' of tunable lasers it is indicated that Newton in his book Opticks was the first to show a diagram using a prism as a beam expander. In the same book he describes, via diagrams, the use of multiple - prism arrays. Some 278 years after Newton's discussion, multiple - prism beam expanders became central to the development of narrow - linewidth tunable lasers. Also, the use of these prismatic beam expanders led to the multiple - prism dispersion theory.

In 1679, Newton returned to his work on (celestial) mechanics, i.e., gravitation and its effect on the orbits of planets, with reference to Kepler's laws of planetary motion. This followed stimulation by a brief exchange of letters in 1679 – 80 with Hooke, who had been appointed to manage the Royal Society's correspondence, and who opened a correspondence intended to elicit contributions from Newton to Royal Society transactions. Newton's reawakening interest in astronomical matters received further stimulus by the appearance of a comet in the winter of 1680 – 1681, on which he corresponded with John Flamsteed. After the exchanges with Hooke, Newton worked out a proof that the elliptical form of planetary orbits would result from a centripetal force inversely proportional to the square of the radius vector (Newton's law of universal gravitation). Newton communicated his results to Edmond Halley and to the Royal Society in De motu corporum in gyrum, a tract written on about 9 sheets which was copied into the Royal Society's Register Book in December 1684. This tract contained the nucleus that Newton developed and expanded to form the Principia.

The Principia was published on 5 July 1687 with encouragement and financial help from Edmond Halley. In this work, Newton stated the three universal laws of motion that enabled many of the advances of the Industrial Revolution which soon followed and were not to be improved upon for more than 200 years, and are still the underpinnings of the non - relativistic technologies of the modern world. He used the Latin word gravitas (weight) for the effect that would become known as gravity, and defined the law of universal gravitation.

In the same work, Newton presented a calculus - like method of geometrical analysis by 'first and last ratios', gave the first analytical determination (based on Boyle's law) of the speed of sound in air, inferred the oblateness of the spheroidal figure of the Earth, accounted for the precession of the equinoxes as a result of the Moon's gravitational attraction on the Earth's oblateness, initiated the gravitational study of the irregularities in the motion of the moon, provided a theory for the determination of the orbits of comets, and much more.

Newton made clear his heliocentric view of the solar system – developed in a somewhat modern way, because already in the mid 1680s he recognized the "deviation of the Sun" from the center of gravity of the solar system. For Newton, it was not precisely the center of the Sun or any other body that could be considered at rest, but rather "the common centre of gravity of the Earth, the Sun and all the Planets is to be esteem'd the Centre of the World", and this center of gravity "either is at rest or moves uniformly forward in a right line" (Newton adopted the "at rest" alternative in view of common consent that the center, wherever it was, was at rest).

Newton's postulate of an invisible force able to act over vast distances led to him being criticized for introducing "occult agencies" into science. Later, in the second edition of the Principia (1713), Newton firmly rejected such criticisms in a concluding General Scholium, writing that it was enough that the phenomena implied a gravitational attraction, as they did; but they did not so far indicate its cause, and it was both unnecessary and improper to frame hypotheses of things that were not implied by the phenomena. (Here Newton used what became his famous expression Hypotheses non fingo).

With the Principia, Newton became internationally recognized. He acquired a circle of admirers, including the Swiss born mathematician Nicolas Fatio de Duillier, with whom he formed an intense relationship that lasted until 1693, when it abruptly ended, at the same time that Newton suffered a nervous breakdown.

In the 1690s, Newton wrote a number of religious tracts dealing with the literal interpretation of the Bible. Henry More's belief in the Universe and rejection of Cartesian dualism may have influenced Newton's religious ideas. A manuscript he sent to John Locke in which he disputed the existence of the Trinity was never published. Later works – The Chronology of Ancient Kingdoms Amended (1728) and Observations Upon the Prophecies of Daniel and the Apocalypse of St. John (1733) – were published after his death. He also devoted a great deal of time to alchemy.

Newton was also a member of the Parliament of England from 1689 to 1690 and in 1701, but according to some accounts his only comments were to complain about a cold draught in the chamber and request that the window be closed.

Newton moved to London to take up the post of warden of the Royal Mint in 1696, a position that he had obtained through the patronage of Charles Montagu, 1st Earl of Halifax, then Chancellor of the Exchequer. He took charge of England's great recoining, somewhat treading on the toes of Lord Lucas, Governor of the Tower (and securing the job of deputy comptroller of the temporary Chester branch for Edmond Halley). Newton became perhaps the best known Master of the Mint upon the death of Thomas Neale in 1699, a position Newton held for the last 30 years of his life. These appointments were intended as sinecures, but Newton took them seriously, retiring from his Cambridge duties in 1701, and exercising his power to reform the currency and punish clippers and counterfeiters. As Master of the Mint in 1717 in the "Law of Queen Anne" Newton moved the Pound Sterling de facto from the silver standard to the gold standard by setting the bimetallic relationship between gold coins and the silver penny in favor of gold. This caused silver sterling coin to be melted and shipped out of Britain. Newton was made President of the Royal Society in 1703 and an associate of the French Académie des Sciences. In his position at the Royal Society, Newton made an enemy of John Flamsteed, the Astronomer Royal, by prematurely publishing Flamsteed's Historia Coelestis Britannica, which Newton had used in his studies.

In April 1705, Queen Anne knighted Newton during a royal visit to Trinity College, Cambridge. The knighthood is likely to have been motivated by political considerations connected with the Parliamentary election in May 1705, rather than any recognition of Newton's scientific work or services as Master of the Mint. Newton was the second scientist to be knighted, after Sir Francis Bacon.

Towards the end of his life, Newton took up residence at Cranbury Park, near Winchester with his niece and her husband, until his death in 1727. His half - niece, Catherine Barton Conduitt, served as his hostess in social affairs at his house on Jermyn Street in London; he was her "very loving Uncle," according to his letter to her when she was recovering from smallpox.

Newton died in his sleep in London on 31 March 1727 [OS: 20 March 1726], and was buried in Westminster Abbey. Newton, a bachelor, had divested much of his estate to relatives during his last years, and died intestate. After his death, Newton's hair was examined and found to contain mercury, probably resulting from his alchemical pursuits. Mercury poisoning could explain Newton's eccentricity in late life.

French mathematician Joseph  -Louis Lagrange often said that Newton was the greatest genius who ever lived, and once added that Newton was also "the most fortunate, for we cannot find more than once a system of the world to establish." English poet Alexander Pope was moved by Newton's accomplishments to write the famous epitaph:

Nature and nature's laws lay hid in night;
God said "Let Newton be" and all was light.

Newton himself had been rather more modest of his own achievements, famously writing in a letter to Robert Hooke in February 1676:

If I have seen further it is by standing on the shoulders of giants.

Two writers think that the above quote, written at a time when Newton and Hooke were in dispute over optical discoveries, was an oblique attack on Hooke (said to have been short and hunchbacked), rather than – or in addition to – a statement of modesty. On the other hand, the widely known proverb about standing on the shoulders of giants published among others by 17th century poet George Herbert (a former orator of the University of Cambridge and fellow of Trinity College) in his Jacula Prudentum (1651), had as its main point that "a dwarf on a giant's shoulders sees farther of the two", and so its effect as an analogy would place Newton himself rather than Hooke as the 'dwarf'.

In a later memoir, Newton wrote:

I do not know what I may appear to the world, but to myself I seem to have been only like a boy playing on the sea - shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me.

Albert Einstein kept a picture of Newton on his study wall alongside ones of Michael Faraday and James Clerk Maxwell. Newton remains influential to today's scientists, as demonstrated by a 2005 survey of members of Britain's Royal Society (formerly headed by Newton) asking who had the greater effect on the history of science, Newton or Einstein. Royal Society scientists deemed Newton to have made the greater overall contribution. In 1999, an opinion poll of 100 of today's leading physicists voted Einstein the "greatest physicist ever;" with Newton the runner up, while a parallel survey of rank - and - file physicists by the site PhysicsWeb gave the top spot to Newton.

Newton's monument (1731) can be seen in Westminster Abbey, at the north of the entrance to the choir against the choir screen, near his tomb. It was executed by the sculptor Michael Rysbrack (1694 – 1770) in white and grey marble with design by the architect William Kent. The monument features a figure of Newton reclining on top of a sarcophagus, his right elbow resting on several of his great books and his left hand pointing to a scroll with a mathematical design. Above him is a pyramid and a celestial globe showing the signs of the Zodiac and the path of the comet of 1680. A relief panel depicts putti using instruments such as a telescope and prism. The Latin inscription on the base translates as:

Here is buried Isaac Newton, Knight, who by a strength of mind almost divine, and mathematical principles peculiarly his own, explored the course and figures of the planets, the paths of comets, the tides of the sea, the dissimilarities in rays of light, and, what no other scholar has previously imagined, the properties of the colours thus produced. Diligent, sagacious and faithful, in his expositions of nature, antiquity and the holy Scriptures, he vindicated by his philosophy the majesty of God mighty and good, and expressed the simplicity of the Gospel in his manners. Mortals rejoice that there has existed such and so great an ornament of the human race! He was born on 25 December 1642, and died on 20 March 1726/7. — Translation from G.L. Smyth, The Monuments and Genii of St. Paul's Cathedral, and of Westminster Abbey (1826), ii, 703–4.

From 1978 until 1988, an image of Newton designed by Harry Ecclestone appeared on Series D £1 banknotes issued by the Bank of England (the last £1 notes to be issued by the Bank of England). Newton was shown on the reverse of the notes holding a book and accompanied by a telescope, a prism and a map of the Solar System.

A statue of Isaac Newton, looking at an apple at his feet, can be seen at the Oxford University Museum of Natural History.

According to most scholars, Newton was a monotheist who believed in biblical prophecies but was Antitrinitarian. 'In Newton's eyes, worshiping Christ as God was idolatry, to him the fundamental sin'. Historian Stephen D. Snobelen says of Newton, "Isaac Newton was a heretic. But ... he never made a public declaration of his private faith — which the orthodox would have deemed extremely radical. He hid his faith so well that scholars are still unraveling his personal beliefs." Snobelen concludes that Newton was at least a Socinian sympathizer (he owned and had thoroughly read at least eight Socinian books), possibly an Arian and almost certainly an anti - trinitarian. In an age notable for its religious intolerance, there are few public expressions of Newton's radical views, most notably his refusal to take holy orders and his refusal, on his death bed, to take the sacrament when it was offered to him.

In a view disputed by Snobelen, T.C. Pfizenmaier argues that Newton held the Arian view of the Trinity rather than the Western one held by Roman Catholics, Anglicans and most Protestants. Although the laws of motion and universal gravitation became Newton's best known discoveries, he warned against using them to view the Universe as a mere machine, as if akin to a great clock. He said, "Gravity explains the motions of the planets, but it cannot explain who set the planets in motion. God governs all things and knows all that is or can be done."

Along with his scientific fame, Newton's studies of the Bible and of the early Church Fathers were also noteworthy. Newton wrote works on textual criticism, most notably An Historical Account of Two Notable Corruptions of Scripture. He placed the crucifixion of Jesus Christ at 3 April, AD 33, which agrees with one traditionally accepted date. He also tried unsuccessfully to find hidden messages within the Bible.

Newton wrote more on religion than he did on natural science. He believed in a rationally immanent world, but he rejected the hylozoism implicit in Leibniz and Baruch Spinoza. The ordered and dynamically informed Universe could be understood, and must be understood, by an active reason. In his correspondence, Newton claimed that in writing the Principia "I had an eye upon such Principles as might work with considering men for the belief of a Deity". He saw evidence of design in the system of the world: "Such a wonderful uniformity in the planetary system must be allowed the effect of choice". But Newton insisted that divine intervention would eventually be required to reform the system, due to the slow growth of instabilities. For this, Leibniz lampooned him: "God Almighty wants to wind up his watch from time to time: otherwise it would cease to move. He had not, it seems, sufficient foresight to make it a perpetual motion." Newton's position was vigorously defended by his follower Samuel Clarke in a famous correspondence. A century later, Pierre - Simon Laplace's work "Celestial Mechanics" had a natural explanation for why the planet orbits don't require periodic divine intervention.

Newton and Robert Boyle's mechanical philosophy was promoted by rationalist pamphleteers as a viable alternative to the pantheists and enthusiasts, and was accepted hesitantly by orthodox preachers as well as dissident preachers like the latitudinarians. The clarity and simplicity of science was seen as a way to combat the emotional and metaphysical superlatives of both superstitious enthusiasm and the threat of atheism, and at the same time, the second wave of English deists used Newton's discoveries to demonstrate the possibility of a "Natural Religion".

The attacks made against pre - Enlightenment "magical thinking", and the mystical elements of Christianity, were given their foundation with Boyle's mechanical conception of the Universe. Newton gave Boyle's ideas their completion through mathematical proofs and, perhaps more importantly, was very successful in popularizing them. Newton refashioned the world governed by an interventionist God into a world crafted by a God that designs along rational and universal principles. These principles were available for all people to discover, allowed people to pursue their own aims fruitfully in this life, not the next, and to perfect themselves with their own rational powers.

Newton saw God as the master creator whose existence could not be denied in the face of the grandeur of all creation. His spokesman, Clarke, rejected Leibniz' theodicy which cleared God from the responsibility for l'origine du mal by making God removed from participation in his creation, since as Clarke pointed out, such a deity would be a king in name only, and but one step away from atheism. But the unforeseen theological consequence of the success of Newton's system over the next century was to reinforce the deist position advocated by Leibniz. The understanding of the world was now brought down to the level of simple human reason, and humans, as Odo Marquard argued, became responsible for the correction and elimination of evil.

In a manuscript he wrote in 1704 in which he describes his attempts to extract scientific information from the Bible, he estimated that the world would end no earlier than 2060. In predicting this he said, "This I mention not to assert when the time of the end shall be, but to put a stop to the rash conjectures of fanciful men who are frequently predicting the time of the end, and by doing so bring the sacred prophesies into discredit as often as their predictions fail."

Enlightenment philosophers chose a short history of scientific predecessors — Galileo, Boyle and Newton principally — as the guides and guarantors of their applications of the singular concept of Nature and Natural Law to every physical and social field of the day. In this respect, the lessons of history and the social structures built upon it could be discarded.

It was Newton's conception of the Universe based upon Natural and rationally understandable laws that became one of the seeds for Enlightenment ideology. Locke and Voltaire applied concepts of Natural Law to political systems advocating intrinsic rights; the physiocrats and Adam Smith applied Natural conceptions of psychology and self - interest to economic systems; and sociologists criticized the current social order for trying to fit history into Natural models of progress. Monboddo and Samuel Clarke resisted elements of Newton's work, but eventually rationalized it to conform with their strong religious views of nature.

As warden of the Royal Mint, Newton estimated that 20 percent of the coins taken in during The Great Recoinage of 1696 were counterfeit. Counterfeiting was high treason, punishable by the felon's being hanged, drawn and quartered. Despite this, convicting the most flagrant criminals could be extremely difficult. However, Newton proved to be equal to the task. Disguised as a habitué of bars and taverns, he gathered much of that evidence himself. For all the barriers placed to prosecution, and separating the branches of government, English law still had ancient and formidable customs of authority. Newton had himself made a justice of the peace in all the home counties - there is a draft of a letter regarding this matter stuck into Newton's personal first edition of his Philosophiæ Naturalis Principia Mathematica which he must have been amending at the time. Then he conducted more than 100 cross examinations of witnesses, informers, and suspects between June 1698 and Christmas 1699. Newton successfully prosecuted 28 coiners.

One of Newton's cases as the King's attorney was against William Chaloner. Chaloner's schemes included setting up phony conspiracies of Catholics and then turning in the hapless conspirators whom he had entrapped. Chaloner made himself rich enough to posture as a gentleman. Petitioning Parliament, Chaloner accused the Mint of providing tools to counterfeiters (a charge also made by others). He proposed that he be allowed to inspect the Mint's processes in order to improve them. He petitioned Parliament to adopt his plans for a coinage that could not be counterfeited, while at the same time striking false coins. Newton put Chaloner on trial for counterfeiting and had him sent to Newgate Prison in September 1697. But Chaloner had friends in high places, who helped him secure an acquittal and his release. Newton put him on trial a second time with conclusive evidence. Chaloner was convicted of high treason and hanged, drawn and quartered on 23 March 1699 at Tyburn gallows.

The famous three laws of motion (stated in modernized form): Newton's First Law (also known as the Law of Inertia) states that an object at rest tends to stay at rest and that an object in uniform motion tends to stay in uniform motion unless acted upon by a net external force. The meaning of this law is the existence of reference frames (called inertial frames) where objects not acted upon by forces move in uniform motion (in particular, they may be at rest).

Newton's Second Law states that an applied force, 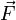, on an object equals the rate of change of its momentum, 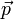, with time. Mathematically, this is expressed as

If applied to an object with constant mass (dm/dt = 0), the first term vanishes, and by substitution using the definition of acceleration, the equation can be written in the iconic form

The first and second laws represent a break with the physics of Aristotle, in which it was believed that a force was necessary in order to maintain motion. They state that a force is only needed in order to change an object's state of motion. The SI unit of force is the newton, named in Newton's honor.

Newton's Third Law states that for every action there is an equal and opposite reaction. This means that any force exerted onto an object has a counterpart force that is exerted in the opposite direction back onto the first object. A common example is of two ice skaters pushing against each other and sliding apart in opposite directions. Another example is the recoil of a firearm, in which the force propelling the bullet is exerted equally back onto the gun and is felt by the shooter. Since the objects in question do not necessarily have the same mass, the resulting acceleration of the two objects can be different (as in the case of firearm recoil).

Unlike Aristotle's, Newton's physics is meant to be universal. For example, the second law applies both to a planet and to a falling stone.

The vector nature of the second law addresses the geometrical relationship between the direction of the force and the manner in which the object's momentum changes. Before Newton, it had typically been assumed that a planet orbiting the Sun would need a forward force to keep it moving. Newton showed instead that all that was needed was an inward attraction from the Sun. Even many decades after the publication of the Principia, this counter - intuitive idea was not universally accepted, and many scientists preferred Descartes' theory of vortices.

Newton himself often told the story that he was inspired to formulate his theory of gravitation by watching the fall of an apple from a tree. Although it has been said that the apple story is a myth and that he did not arrive at his theory of gravity in any single moment, acquaintances of Newton (such as William Stukeley, whose manuscript account, published in 1752, has been made available by the Royal Society) do in fact confirm the incident, though not the cartoon version that the apple actually hit Newton's head. Stukeley recorded in his Memoirs of Sir Isaac Newton's Life a conversation with Newton in Kensington on 15 April 1726:

... We went into the garden, & drank tea under the shade of some appletrees, only he, & myself. amidst other discourse, he told me, he was just in the same situation, as when formerly, the notion of gravitation came into his mind. "why should that apple always descend perpendicularly to the ground," thought he to him self: occasion'd by the fall of an apple, as he sat in a comtemplative mood: "why should it not go sideways, or upwards? but constantly to the earths centre? assuredly, the reason is, that the earth draws it. there must be a drawing power in matter. & the sum of the drawing power in the matter of the earth must be in the earths centre, not in any side of the earth. therefore dos this apple fall perpendicularly, or toward the centre. if matter thus draws matter; it must be in proportion of its quantity. therefore the apple draws the earth, as well as the earth draws the apple."

John Conduitt, Newton's assistant at the Royal Mint and husband of Newton's niece, also described the event when he wrote about Newton's life:

In the year 1666 he retired again from Cambridge to his mother in Lincolnshire. Whilst he was pensively meandering in a garden it came into his thought that the power of gravity (which brought an apple from a tree to the ground) was not limited to a certain distance from earth, but that this power must extend much further than was usually thought. Why not as high as the Moon said he to himself & if so, that must influence her motion & perhaps retain her in her orbit, whereupon he fell a calculating what would be the effect of that supposition.

In similar terms, Voltaire wrote in his Essay on Epic Poetry (1727), "Sir Isaac Newton walking in his gardens, had the first thought of his system of gravitation, upon seeing an apple falling from a tree."

It is known from his notebooks that Newton was grappling in the late 1660s with the idea that terrestrial gravity extends, in an inverse - square proportion, to the Moon; however it took him two decades to develop the full fledged theory. The question was not whether gravity existed, but whether it extended so far from Earth that it could also be the force holding the Moon to its orbit. Newton showed that if the force decreased as the inverse square of the distance, one could indeed calculate the Moon's orbital period, and get good agreement. He guessed the same force was responsible for other orbital motions, and hence named it "universal gravitation".

Various trees are claimed to be "the" apple tree which Newton describes. The King's School, Grantham, claims that the tree was purchased by the school, uprooted and transported to the headmaster's garden some years later. The staff of the [now] National Trust owned Woolsthorpe Manor dispute this, and claim that a tree present in their gardens is the one described by Newton. A descendant of the original tree can be seen growing outside the main gate of Trinity College, Cambridge, below the room Newton lived in when he studied there. The National Fruit Collection at Brogdale can supply grafts from their tree, which appears identical to Flower of Kent, a coarse fleshed cooking variety.