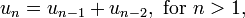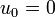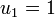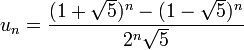<Back to Index>
- Mathematician and
Physicist Jacques
Philippe Marie Binet, 1786
PAGE SPONSOR
Jacques Philippe Marie Binet (February 2, 1786 – May 12, 1856) was a French mathematician, physicist and astronomer born in Rennes; he died in Paris, France, in 1856. He made significant contributions to number theory, and the mathematical foundations of matrix algebra which would later lead to important contributions by Cayley and others. In his memoir on the theory of the conjugate axis and of the moment of inertia of bodies he enumerated the principle now known as Binet's theorem. He is also recognized as the first to describe the rule for multiplying matrices in 1812, and Binet's formula expressing Fibonacci numbers in closed form is named in his honor, although the same result was known to Abraham de Moivre a century earlier.
Binet graduated from the École Polytechnique in 1806, and
returned as a teacher in 1807. He advanced in position
until 1816 when he became an inspector of studies at the
École. He held this post until November 13, 1830, when he
was dismissed by the recently crowned King Louis - Philippe of
France, probably because of Binet's strong support of the
previous King, Charles X. In 1823 Binet succeeded Delambre in the chair of
astronomy at the Collège de France. He was made a
Chevalier in the Légion
d'Honneur in 1821, and was elected to the Académie des Sciences in
1843.
Binet's formula provides the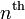 
term in the Fibonacci
sequence, and is defined using the recurrence
formula:
where
