• Mathematician Arthur Cayley, 1821
• Mathematician Giuseppe Peano, 1821

As a child, Cayley enjoyed solving complex math problems for amusement. He entered Trinity College, Cambridge, where he excelled in Greek, French, German and Italian, as well as mathematics. He worked as a lawyer for 14 years.

He postulated the Cayley – Hamilton theorem — that every square matrix is a root of its own characteristic polynomial, and verified it for matrices of order 2 and 3. He was the first to define the concept of a group in the modern way — as a set with a binary operation satisfying certain laws. Formerly, when mathematicians spoke of "groups", they had meant permutation groups.

Arthur Cayley was born in Richmond, London, England, on 16 August 1821. His father, Henry Cayley, was a distant cousin of Sir George Cayley the aeronautics engineer innovator, and descended from an ancient Yorkshire family. He settled in Saint Petersburg, Russia, as a merchant. His mother was Maria Antonia Doughty, daughter of William Doughty. According to some writers she was Russian, but her father's name indicates an English origin. His brother was the linguist Charles Bagot Cayley. Arthur spent his first eight years in Saint Petersburg. In 1829 his parents were settled permanently at Blackheath, near London. Arthur was sent to a private school. He early showed great liking for, and aptitude in, numerical calculation. At age 14 he was sent to King's College School. The school's master observed indications of mathematical genius and advised the father to educate his son not for his own business, as he had intended, but to enter the University of Cambridge.

At the unusually early age of 17 Cayley began residence at Trinity College, Cambridge. The cause of the Analytical Society had now triumphed, and the Cambridge Mathematical Journal had been instituted by Gregory and Robert Leslie Ellis. To this journal, at the age of twenty, Cayley contributed three papers, on subjects which had been suggested by reading the Mécanique analytique of Lagrange and some of the works of Laplace.

Cayley's tutor at Cambridge was George Peacock and his private coach was William Hopkins. He finished his undergraduate course by winning the place of Senior Wrangler, and the first Smith's prize. His next step was to take the M.A. degree, and win a Fellowship by competitive examination. He continued to reside at Cambridge for four years; during which time he took some pupils, but his main work was the preparation of 28 memoirs to the Mathematical Journal.

Because of the limited tenure of his fellowship it was necessary to choose a profession; like De Morgan, Cayley chose law, and at age 25 entered at Lincoln's Inn, London. He made a specialty of conveyancing. It was while he was a pupil at the bar examination that he went to Dublin to hear Hamilton's lectures on quaternions.

His friend Sylvester, his senior by five years at Cambridge, was then an actuary, resident in London; they used to walk together round the courts of Lincoln's Inn, discussing the theory of invariants and covariants. During this period of his life, extending over fourteen years, Cayley produced between two and three hundred papers.

At Cambridge University the ancient professorship of pure mathematics is denominated the Lucasian, and is the chair which had been occupied by Isaac Newton. Around 1860, certain funds bequeathed by Lady Sadleir to the University, having become useless for their original purpose, were employed to establish another professorship of pure mathematics, called the Sadleirian. The duties of the new professor were defined to be "to explain and teach the principles of pure mathematics and to apply himself to the advancement of that science." To this chair Cayley was elected when 42 years old. He gave up a lucrative practice for a modest salary; but he never regretted the exchange, for the chair at Cambridge enabled him to end the divided allegiance between law and mathematics, and to devote his energies to the pursuit which he liked best. He at once married and settled down in Cambridge. More fortunate than Hamilton in his choice, his home life was one of great happiness. His friend and fellow investigator, Sylvester, once remarked that Cayley had been much more fortunate than himself; that they both lived as bachelors in London, but that Cayley had married and settled down to a quiet and peaceful life at Cambridge; whereas he had never married, and had been fighting the world all his days.

At first the teaching duty of the Sadleirian professorship was limited to a course of lectures extending over one of the terms of the academic year; but when the University was reformed about 1886, and part of the college funds applied to the better endowment of the University professors, the lectures were extended over two terms. For many years the attendance was small, and came almost entirely from those who had finished their career of preparation for competitive examinations; after the reform the attendance numbered about fifteen. The subject lectured on was generally that of the memoir on which the professor was for the time engaged.

The other duty of the chair — the advancement of mathematical science — was discharged in a handsome manner by the long series of memoirs which he published, ranging over every department of pure mathematics. But it was also discharged in a much less obtrusive way; he became the standing referee on the merits of mathematical papers to many societies both at home and abroad.

In 1876 he published a Treatise on Elliptic Functions, which was his only book. He took great interest in the movement for the University education of women. At Cambridge the women's colleges are Girton and Newnham. In the early days of Girton College he gave direct help in teaching, and for some years he was chairman of the council of Newnham College, in the progress of which he took the keenest interest to the last.

In 1872 he was made an honorary fellow of Trinity College, and three years later an ordinary fellow, which meant stipend as well as honor. About this time his friends subscribed for a presentation portrait. Maxwell wrote an address to the committee of subscribers who had charge of the Cayley portrait fund. The verses refer to the subjects investigated in several of Cayley's most elaborate memoirs; such as, Chapters on the Analytical Geometry of 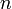dimensions; On the theory of Determinants; Memoir on the theory of Matrices; Memoirs on skew surfaces, otherwise Scrolls; On the delineation of a Cubic Scroll, etc.

In 1881 he received from the Johns Hopkins University, Baltimore, where Sylvester was then professor of mathematics, an invitation to deliver a course of lectures. He accepted the invitation, and lectured at Baltimore during the first five months of 1882 on the subject of the Abelian and Theta Functions.

In 1883 Cayley was President of the British Association for the Advancement of Science. The meeting was held at Southport, in the north of England. As the President's address is one of the great popular events of the meeting, and brings out an audience of general culture, it is usually made as little technical as possible. Cayley (1996) took for his subject the Progress of Pure Mathematics.

In 1889 the Cambridge University Press requested him to prepare his mathematical papers for publication in a collected form — a request which he appreciated very much. They are printed in magnificent quarto volumes, of which seven appeared under his own editorship. While editing these volumes, he was suffering from a painful internal malady, to which he succumbed on 26 January 1895, in the 74th year of his age. When the funeral took place, a great assemblage met in Trinity Chapel, comprising members of the University, official representatives of Russia and America, and many of the most illustrious philosophers of Britain.

The remainder of his papers were edited by Andrew Forsyth, his successor in the Sadleirian Chair. The Collected Mathematical papers number thirteen quarto volumes, and contain 967 papers. Cayley retained to the last his fondness for novel reading and for traveling. He also took special pleasure in paintings and architecture, and he practiced water color painting, which he found useful sometimes in making mathematical diagrams.

In 1887, Peano married Carola Crosio, the daughter of the Turin based painter Luigi Crosio, known for painting the Refugium Peccatorum Madonna. In 1886, he began teaching concurrently at the Royal Military Academy, and was promoted to Professor First Class in 1889. The next year, the University of Turin also granted him his full professorship. Peano's famous space filling curve appeared in 1890 as a counterexample. He used it to show that a continuous curve cannot always be enclosed in an arbitrarily small region. This was an early example of what came to be known as a fractal.

The following year Peano started the Formulario Project. It was to be an "Encyclopedia of Mathematics", containing all known formulae and theorems of mathematical science using a standard notation invented by Peano. In 1897, the first International Congress of Mathematicians was held in Zürich. Peano was a key participant, presenting a paper on mathematical logic. He also started to become increasingly occupied with Formulario to the detriment of his other work.

In 1898 he presented a note to the Academy about binary numeration and its ability to be used to represent the sounds of languages. He also became so frustrated with publishing delays (due to his demand that formulae be printed on one line) that he purchased a printing press.

Paris was the venue for the Second International Congress of Mathematicians in 1900. The conference was preceded by the First International Conference of Philosophy where Peano was a member of the patronage committee. He presented a paper which posed the question of correctly formed definitions in mathematics, i.e.. "how do you define a definition?". This became one of Peano's main philosophical interests for the rest of his life. At the conference Peano met Bertrand Russell and gave him a copy of Formulario. Russell was so struck by Peano's innovative logical symbols that he left the conference and returned home to study Peano's text.

Peano's students Mario Pieri and Alessandro Padoa had papers presented at the philosophy congress also. For the mathematical congress, Peano did not speak, but Padoa's memorable presentation has been frequently recalled. A resolution calling for the formation of an "international auxiliary language" to facilitate the spread of mathematical (and commercial) ideas, was proposed; Peano fully supported it.

By 1901, Peano was at the peak of his mathematical career. He had made advances in the areas of analysis, foundations and logic, made many contributions to the teaching of calculus and also contributed to the fields of differential equations and vector analysis. Peano played a key role in the axiomatization of mathematics and was a leading pioneer in the development of mathematical logic. Peano had by this stage become heavily involved with the Formulario project and his teaching began to suffer. In fact, he became so determined to teach his new mathematical symbols that the calculus in his course was neglected. As a result he was dismissed from the Royal Military Academy but retained his post at Turin University.

In 1903 Peano announced his work on an international auxiliary language called Latino sine flexione ("Latin without inflexion," later called Interlingua, but which should not be confused with the later Interlingua of the IALA). This was an important project for him (along with finding contributors for 'Formulario'). The idea was to use Latin vocabulary, since this was widely known, but simplify the grammar as much as possible and remove all irregular and anomalous forms to make it easier to learn. In one speech, he started speaking in Latin and, as he described each simplification, introduced it into his speech so that by the end he was talking in his new language.

The year 1908 was big for Peano. The fifth and final edition of the Formulario project, titled Formulario Mathematico, was published. It contained 4200 formulae and theorems, all completely stated and most of them proved. The book received little attention since much of the content was dated by this time. However, it remains a significant contribution to mathematical literature. The comments and examples were written in Latino sine flexione.

Also in 1908, Peano took over the chair of higher analysis at Turin (this appointment was to last for only two years). He was elected the director of Academia pro Interlingua. Having previously created Idiom Neutral, the Academy effectively chose to abandon it in favor of Peano's Latino sine flexione.

After his mother died in 1910, Peano divided his time between teaching, working on texts aimed for secondary schooling including a dictionary of mathematics, and developing and promoting his and other auxiliary languages, becoming a revered member of the international auxiliary language movement. He used his membership of the Accademia dei Lincei to present papers written by friends and colleagues who were not members (the Accademia recorded and published all presented papers given in sessions).

In 1925 Peano switched Chairs unofficially from Infinitesimal Calculus to Complementary Mathematics, a field which better suited his current style of mathematics. This move became official in 1931. Giuseppe Peano continued teaching at Turin University until the day before he died, when he suffered a fatal heart attack.