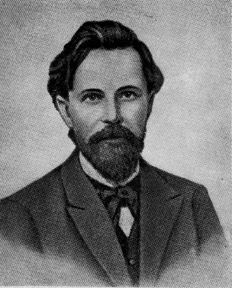
Andrey (Andrei) Andreyevich Markov (Russian: Андре́й Андре́евич Ма́рков) (June 14, 1856 N.S. – July 20, 1922) was a Russian mathematician. He is best known for his work on theory of stochastic processes. A primary subject of his research later became known as Markov chains.

He and his younger brother Vladimir Andreevich Markov (1871 – 1897) proved Markov brothers' inequality. His son, another Andrey Andreevich Markov (1903 – 1979), was also a notable mathematician, making contributions on constructive mathematics and recursive function theory.

Andrey Andreyevich Markov was born in Ryazan as the son of the secretary of the public forest management of Ryazan, Andrey Grigorevich Markov, and his first wife Nadezhda Petrovna Markova.

In the beginning of the 1860s Andrey Grigorevich moved to St. Petersburg to become an asset manager of the princess Ekaterina Aleksandrovna Valvatyeva.

In 1866 Andrey Andreevich's school life began with his entrance into St. Petersburg's fifth grammar school. Already during his school time Andrey was intensely engaged in higher mathematics. As a 17 year old grammar school student he informed Bunyakovsky, Korkin and Yegor Zolotarev about an apparently new method to solve linear ordinary differential equations and was invited to the so-called Korkin Saturdays, where Korkin's students regularly met. In 1874 he finished the school and began his studies at the physico - mathematical faculty of St. Petersburg University.

Among his teachers were Yulian Sokhotski (differential calculus, higher algebra), Konstantin Posse (analytic geometry), Yegor Zolotarev (integral calculus), Pafnuty Chebyshev (number theory, probability theory), Aleksandr Korkin (ordinary and partial differential equations), Okatov (mechanism theory),Osip Somov (mechanics) and Budaev (descriptive and higher geometry).

In 1877 he was awarded the gold medal for his outstanding solution of the problem "About Integration of Differential Equations by Continuous Fractions with an Application to the Equation 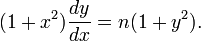" In the following year he passed the candidate examinations and remained at the university to prepare for the lecturer's position.

In April 1880 Markov defended his Master's thesis "About Binary Quadratic Forms with Positive Determinant", which was encouraged by Aleksandr Korkin and Yegor Zolotarev.

Five years later, in January 1885, there followed his doctoral thesis "About Some Applications of Algebraic Continuous Fractions".

His pedagogical work began after the defense of his Master's thesis in autumn 1880. As a privatdozent he lectured on differential and integral calculus. Later he lectured alternately on "introduction to analysis", probability theory (succeeding Chebyshev who had left the university in 1882) and calculus of differences. From 1895 - 96 until 1905 he also lectured on differential calculus.

One year after the defense of his doctoral thesis, he was appointed extraordinary professor (1886) and in the same year he was elected adjunct to the Academy of Sciences. In 1890, after the death of Viktor Bunyakovsky, Markov became an extraordinary member of the academy. His promotion to an ordinary professor of St Petersburg University followed in autumn 1894.

In 1896, he was elected an ordinary member of the academy as the successor of Chebyshev. In 1905 he was appointed merited professor and was granted the right to retire, which he did immediately. Until 1910, however, he continued to lecture on the calculus of differences.

In connection with the student riots in 1908, professors and lecturers of St. Petersburg University were ordered to monitor their students. Markov refused to accept this decree and wrote an explanation in which he declined to be an "agent of the governance". Markov was rejected from further teaching activity at St. Petersburg University, and he eventually decided to retire from the university.

In 1913 the council of St. Petersburg elected nine scientists honorary members of the university. Markov was among them, but his election was not affirmed by the minister of education. The affirmation only occurred four years later, after the February revolution in 1917. Markov then resumed his teaching activities and lectured on probability theory and the calculus of differences until his death in 1922.

In 1912, Markov, protesting Leo Tolstoy's excommunication from the Russian Orthodox Church, requested that he himself be excommunicated. In response, the Church formally excommunicated him.

Kolmogorov was born at Tambov in 1903. His unwed mother died in childbirth and he was raised by his aunts in Tunoshna near Yaroslavl at the estate of his grandfather, a wealthy nobleman. His father, an agronomist by trade, was deported from Saint Petersburg for participation in the revolutionary movement. He disappeared and was presumed to have been killed in the Russian Civil War.

Kolmogorov was educated in his aunt's village school, and his earliest literary efforts and mathematical papers were printed in the school newspaper. As an adolescent he designed perpetual motion machines, concealing their (necessary) defects so cleverly that his secondary school teachers could not discover them. In 1910, his aunt adopted him and then they moved to Moscow, where he went to a gymnasium, graduating from it in 1920.

In 1920, Kolmogorov began to study at the Moscow State University and the Chemistry Technological Institute.

Kolmogorov gained a reputation for his wide ranging erudition. As an undergraduate, he participated in the seminars of the Russian historian S.V. Bachrushin, and he published his first research paper on the landholding practices in the Novgorod Republic in the fifteenth and sixteenth centuries. At the same time (1921 – 1922), Kolmogorov derived and proved several results in set theory and in the theory of Fourier series (trigonometrical series).

In 1922 Kolmogorov constructed a Fourier series that diverges almost everywhere, gaining international recognition. Around this time he decided to devote his life to mathematics. In 1925 Kolmogorov graduated from Moscow State University, and began to study under the supervision of Nikolai Luzin. He made lifelong friends with Pavel Alexandrov who involved Kolmogorov in 1936 in an ugly political persecution of their common teacher, the so-called Luzin case or Luzin affair. Kolmogorov (together with A. Khinchin) became interested in probability theory. Also in 1925, he published his famous work in intuitionistic logic — On the principle of the excluded middle, where he proved that under a certain interpretation all statements of classical formal logic can be formulated as those of intuitionistic logic. In 1929 Kolmogorov earned his Doctor of Philosophy degree, Ph.D., at the Moscow State University.

In 1930, Kolmogorov went on his first long trip abroad, traveling to Göttingen and Munich, Germany, and then to Paris, France. His pioneering work About the Analytical Methods of Probability Theory was published (in German) in 1931. Also in 1931, he became a professor at Moscow University. In 1933, Kolmogorov published the book, Foundations of the Theory of Probability, laying the modern axiomatic foundations of probability theory and establishing his reputation as the world's leading living expert in this field. In 1935, Kolmogorov became the first chairman of probability theory at the Moscow State University. In 1939, he was elected a full member (academician) of the USSR Academy of Sciences. In a 1938 paper, Kolmogorov "established the basic theorems for smoothing and predicting stationary stochastic processes" — a paper that would have major military applications during the Cold War to come. Around the same years (1936) Kolmogorov contributed to the field of ecology and generalized the Lotka - Volterra model of predator - prey systems.

In his study of stochastic processes (random processes), especially Markov processes, Kolmogorov and the British mathematician Sydney Chapman independently developed the pivotal set of equations in the field, the Chapman – Kolmogorov equations.

Later on, Kolmogorov changed his research interests to the area of turbulence, where his publications beginning in 1941 had a significant influence on the field. In classical mechanics, he is best known for the Kolmogorov – Arnold – Moser theorem (first presented in 1954 at the International Congress of Mathematicians). In 1957 he solved a particular interpretation of Hilbert's thirteenth problem (a joint work with his student V. I. Arnold). He was a founder of algorithmic complexity theory, often referred to as Kolmogorov complexity theory, which he began to develop around this time.

Kolmogorov married Anna Dmitrievna Egorova in 1942. He pursued a vigorous teaching routine throughout his life, not only at the university level but also with younger children, as he was actively involved in developing a pedagogy for gifted children, in literature, and in music, as well as in mathematics. At the Moscow State University, Kolmogorov occupied different positions, including the heads of several departments: probability, statistics, and random processes;mathematical logic; and he also served as the Dean of the Moscow State University Faculty of Mechanics and Mathematics.

In 1971, Kolmogorov joined an oceanographic expedition aboard the research vessel Dmitri Mendeleev. He wrote a number of articles for the Great Soviet Encyclopedia. In his later years he devoted much of his effort to the mathematical and philosophical relationship between probability theory in abstract and applied areas.

Kolmogorov died in Moscow in 1987. A quotation, "Every mathematician believes he is ahead over all others. The reason why they don't say this in public, is because they are intelligent people" is attributed to him.