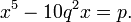He was born of Jewish parentage in Potsdam. He studied at Berlin University, where he obtained the degree of Doctor of Philosophy in 1825, his thesis being an analytical discussion of the theory of fractions. In 1827 he became extraordinary professor and in 1829 ordinary professor of mathematics at Königsberg University, and this chair he filled until 1842.

Jacobi suffered a breakdown from overwork in 1843. He then visited Italy for a few months to regain his health. On his return he moved to Berlin, where he lived as a royal pensioner until his death. During the Revolution of 1848 Jacobi was politically involved and unsuccessfully presented his parliamentary candidature on behalf of a Liberal club. This led, after the suppression of the revolution, to his royal grant being cut off – but his fame and reputation were such that it was soon resumed. In 1836, he was elected a foreign member of the Royal Swedish Academy of Sciences.

Jacobi's grave is preserved at a cemetery in the Kreuzberg section of Berlin, the Friedhof I der Dreifaltigkeits - Kirchengemeinde (61 Baruther Street). His grave is close to that of Johann Encke, the astronomer. The crater Jacobi on the Moon is named after him.

One of Jacobi's greatest accomplishments was his theory of elliptic functions and their relation to the elliptic theta function. This was developed in his great treatise Fundamenta nova theoriae functionum ellipticarum (1829), and in later papers in Crelle's Journal. Theta functions are of great importance in mathematical physics because of their role in the inverse problem for periodic and quasi-periodic flows. The equations of motion are integrable in terms of Jacobi's elliptic functions in the well-known cases of the pendulum, the Euler top, the symmetric Lagrange top in a gravitational field and the Kepler problem (planetary motion in a central gravitational field). He also made fundamental contributions in the study of differential equations and to rational mechanics, notably the Hamilton-Jacobi theory.

It was in algebraic development that Jacobi’s peculiar power mainly lay, and he made important contributions of this kind to many areas of mathematics, as shown by his long list of papers in Crelle’s Journal and elsewhere from 1826 onwards. One of his maxims was: 'Invert, always invert' ('man muss immer umkehren'), expressing his belief that the solution of many hard problems can be clarified by re-expressing them in inverse form.

In his 1835 paper, Jacobi proved the following basic result classifying periodic (including elliptic) functions: If a univariate single-value function is multiply periodic, then such a function cannot have more than two periods and the ratio of the periods cannot be a real number. He discovered many of the fundamental properties of theta functions, including the functional equation and the Jacobi triple product formula, as well as many other results on q-series and hypergeometric series.

The solution of the Jacobi inversion problem for the hyperelliptic Abel map by Weierstrass in 1854 required the introduction of the hyperelliptic theta function and later the general Riemann theta function for algebraic curves of arbitrary genus. The complex torus associated to a genus g algebraic curve, obtained by quotienting  by the lattice of periods is referred to as the Jacobian variety. This method of inversion, and its subsequent extension by Weierstrass and Riemann to arbitrary algebraic curves, may be seen as a higher genus generalization of the relation between elliptic integrals and the Jacobi, or Weierstrass elliptic functions.

Jacobi was the first to apply elliptic functions to number theory, for example proving the 2 square and four-square theorems of Pierre de Fermat, and similar results for 6 and 8 squares. His other work in number theory continued the work of C.F. Gauss: new proofs of quadratic reciprocity and introduction of the Jacobi symbol; contributions to higher reciprocity laws, investigations of continued fractions, and the invention of Jacobi sums.

He was also one of the early founders of the theory of determinants; in particular, he invented the Jacobian determinant formed from the n² differential coefficients of n given functions of n independent variables, and which has played an important part in many analytical investigations. In 1841 he reintroduced the partial derivative ∂ notation of Legendre, which was to become standard.

Students of vector fields and Lie theory often encounter the Jacobi identity, the analog of associativity for the Lie bracket operation.

Planetary theory and other particular dynamical problems likewise occupied his attention from time to time. While contributing to celestial mechanics, he introduced the Jacobi integral (1836) for a sidereal coordinate system. His theory of the last multiplier is treated in Vorlesungen über Dynamik, edited by Alfred Clebsch (1866).

He reduced the general quintic equation to the form: 

He left a vast store of manuscripts, portions of which have been published at intervals in Crelle's Journal. His other works include Commentatio de transformatione integralis duplicis indefiniti in formam simpliciorem (1832), Canon arithmeticus (1839), and Opuscula mathematica (1846 – 1857). His Gesammelte Werke (1881 – 1891) were published by the Berlin Academy.