<Back to Index>
- Mathematician Ferdinand Georg Frobenius, 1849
- Composer Giuseppe Domenico Scarlatti, 1685
- Président de la République Française François Maurice Adrien Marie Mitterrand, 1916
PAGE SPONSOR


Ferdinand Georg Frobenius (October 26, 1849 – August 3, 1917) was a German mathematician, best-known for his contributions to the theory of differential equations and to group theory. He also gave the first full proof for the Cayley–Hamilton theorem.
Frobenius was born in Charlottenburg, a suburb of Berlin, and was educated at the University of Berlin. His thesis, supervised by Weierstrass,
was on the solution of differential equations. After its completion in
1870, he taught in Berlin for a few years before receiving an
appointment at the Polytechnicum in Zurich (now ETH Zurich). In 1893 he returned to Berlin, where he was elected to the Prussian Academy of Sciences. Group theory was
one of Frobenius' principal interests in the second half of his career.
One of his first notable contributions was the proof of the Sylow theorems for abstract groups. Earlier proofs had been for permutation groups. His proof of the first Sylow theorem (on the existence of Sylow groups) is one of those frequently used today. Frobenius also has proved the following fundamental theorem: If a positive integer n divides the order |G| of a finite group G, then the number of solutions of the equation xn = 1 in G is equal to kn for some positive integer k. He also posed the following problem: If, in the above theorem, k = 1, then the solutions of the equation xn = 1 in G form a subgroup. Many years ago this problem was solved for solvable groups. Only in 1991, after the classification of finite simple groups, this problem was solved in general. More important was his creation of the theory of group characters and group representations, which are fundamental tools for studying the structure of groups. This work led to the notion of Frobenius reciprocity and the definition of what are now called Frobenius groups. A group G is said to be a Frobenius group if there is a subgroup H < G such that In that case, the set together with the identity element of G forms a subgroup which is nilpotent as
Thompson has showed in his celebrated PhD thesis. The proof of this
fundamental result showed usefulness of character theory for study of
finite groups. It should be noted that all known proofs of that theorem
make use of characters. In his first paper about characters (1896),
Frobenius constructed the character table of the group PSL(2,p) of order (1/2)(p2 − 1) for all odd primes p (this group is simple provided p > 3). He also made fundamental contributions to the representation theory of the symmetric and alternating groups.
A Russian translation of main Frobenius' papers on character theory with
comments by Prof. Anton K. Sushkewich (he attended Frobenius' lectures
in 1907–1911) was published in 1937 in Kharkov (20 years after his
death).
Frobenius introduced a canonical way of turning primes into conjugacy classes in Galois groups over Q. Specifically, if K/Q is a finite Galois extension then to each (positive) prime p which does not ramify in K and to each prime ideal P lying over p in K there is a unique element g of Gal(K/Q) satisfying the condition g(x) = xp (mod P) for all integers x of K. Varying P over p changes g into a conjugate (and every conjugate of g occurs in this way), so the conjugacy class of g in the Galois group is canonically associated to p. This is called the Frobenius conjugacy class of p and any element of the conjugacy class is called a Frobenius element of p. If we take for K the mth cyclotomic field, whose Galois group over Q is the units modulo m (and thus is abelian, so conjugacy classes become elements), then for p not dividing m the Frobenius class in the Galois group is p mod m. From this point of view, the distribution of Frobenius conjugacy classes in Galois groups over Q (or,
more generally, Galois groups over any number field) generalizes
Dirichlet's classical result about primes in arithmetic progressions.
The study of Galois groups of infinite-degree extensions of Q depends
crucially on this construction of Frobenius elements, which provides in
a sense a dense subset of elements which are accessible to detailed
study.
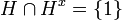 for all
for all 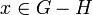 .
.